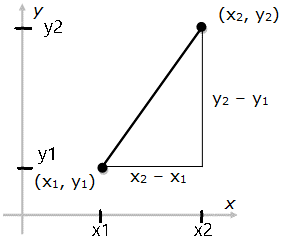Cartesian Coordinates - distance between points on a grid
You can use your knowledge of the pythagorean theorem to find the distance between any two grid points.
Notice that if you plot 2 points on a grid you can make a right triangle, like this:
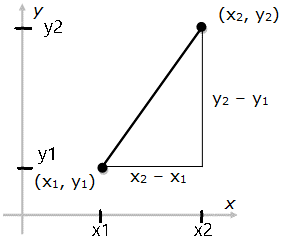
D
The length of the dark line in this graph is the distance between these two points.
That dark line (D) is the hypotenuse of that little right triangle.
Let's call these two points (x1,y1) and (x2,y2).
Here's how you find this distance:
1. Find the distance between the x coordinates: (x2 - x1). Call this dx.
2. Find the distance between the y coordinates: (y2 - y1). Call this dy.
3. By the pythagorean theorem, D, the distance between them (the length of the hypotenuse), is:
D = √
(dx)2 + (dy)2
= √
(x2 - x1)2 + (y2 - y1)2
|
Here's an example:
Find the distance between (+4,+3) and (-2,+1).
Well, the distance between the x points:
(x2 - x1) = +4 - ( - 2) = +4 +2 = 6 (remember: minus times minus = plus)
The distance between the y points:
(y2 - y1) = +3 - (+1) = +3 - 1 = 2 (minus times plus = minus)
So, D =
√
(6 2 +
2 2)
= √
(36 + 4)
= √
40 = 6.3246 (approximately)
|
 |
|