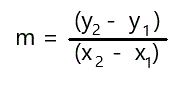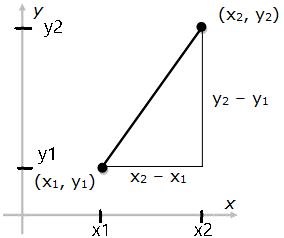Hands-on math!

Cartesian Coordinates - The equation of a line

The equation of a line is:
y = mx + b
where:
y is the y coordinate of a point on the line (any point!)
x is the x coordinate of that same point
m is the slope of the line
    (the change in y divided by the change in x), and
b is the 'y-intercept'
    (the value of y where the line crosses the vertical y axis)

This equation gives you a y-value on the line if you know the corresponding x-value and the other 2 terms, the slope (m) and the y-intercept (b).
If you know the coordinates of 2 points on the line, (x1,y1) and (x2,y2), then you can determine the equation of the line in the y = mx + b form.
Once you have this equation, you can find any point on the line, given either its x or y value.

Here is how you do it:
Call the 2 points you know (x1, y1) and (x2, y2) ====>
  1. Find the slope, m
    This is the change in y: (y2 - y1)
    divided by the change in x: (x2 - x1)
  2. Find the y-intercept, b
    Once you have the slope, m, you find where the line crosses the y axis (that's where x = 0) by just plugging in one of the 2 coordinates and solving for b:
    Let's use (x1, y1):
    y1 = m x1 + b; so
    b = y1 - m x1   (You could just as well used (x2,y2))

Let's try it on an example:

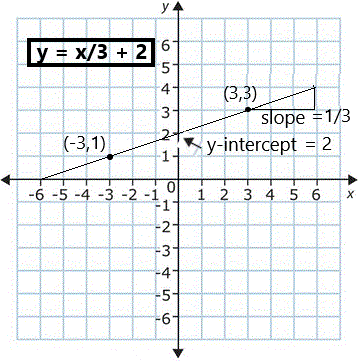
Find the equation of the line that passes through
(-3,1) and (3,3) (see the figure to the right)
  1. Find the slope, m
    Well, the slope, m, is
    m = (3 - 1) / (3 - (-3)) = 2 / 6 = 1 /3
    This means that for every 3 spaces in x,
    you go up 1 in y.
  2. Find the y-intercept, b
    Now, you find the y-intercept (the value of y where this line crosses the y-axis) by just plugging in the values for one of the points.
    We'll use (-3,1) and the slope, (m = 1⁄3) you just found:
        y1 = m x1 + b, so
        b = y1 - m x1
        b = 1 - (1⁄3) (- 3⁄1)     (the 3s cancel each other!)
        b = 1 + 1 = 2;   the line crosses the y-axis at y = +2
So, the equation of the line that passes through
(-3,1) and (3,3) is:
      y = m x +b
      y = (1⁄3) x + 2 or,
      y = x/3 + 2

Try it out! Find out where it crosses the x-axis:
That is where y = 0:
      y = x / 3 + 2
      0 = x / 3 + 2
      x / 3 = -2
      x = (-2) (3) = - 6   It crosses the x axis at x = - 6   ↗

Computing the slope: Direction is important when computing the slope. Its important to pay attention to whether you are moving up or down, going from the left-most point (smaller x) to the right-most point. If you go up to get to your second point, the slope is positive. If you go down to get to your second point, the slope is negative. If you always go from the left-most point (smaller x) to the right-most, then the second y value minus the first y value divided by the difference in their x values will give you the correct slope.
Always remember:
  • Start with the the left-most point (smallest x)
  • Slope goes up: positive slope (UP = +)
  • Slope goes down: negative slope (DOWN = - )
Now, here's a problem for you:
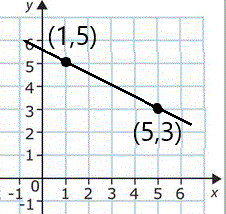Find the slope and the equation of this line:



Slope (m) = _____

Plug in the x and y values for the first point
    (x=1,y=5) into b = y - m x
    to find the y-intercept, b:

b = __________

Equation: y = ____ x + _____