Cartesian Coordinates - Rotations about the Origin
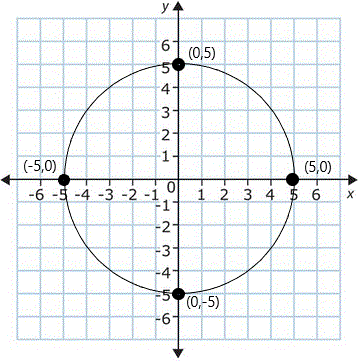Consider the rotations of the point (5,0) around the origin by the following angles:
Original
Coordinates
|
90o
counter-
clockwise
↶
|
180o
|
90o
clockwise
rotation
↷
|
| (5,0)
|
(0,5)
|
(-5,0)
|
(0,-5)
|
The general rule for these rotations is
Original
Coordinates
|
90o
counter-
clockwise
↶
|
180o
|
90o
clockwise
rotation
↷
|
| (x,y)
|
(-y,x)
|
(-x,-y)
|
(y,-x)
|
Please note that a clockwise rotation of 90o is the same as a counter-clockwise rotation of 270o.
To perform a rotation about a point that is NOT the origin:
- Subtract the rotation point from the original point.
This makes the original point relative to the origin so it can be rotated.
- Perform the rotation per the above table.
- Add the rotation point back.
Example: Rotate (3,3) 90o counterclockwise around (1,1):
- Subtract (1,1) from (3,3) = (3-1,3-1) = (2,2)
- Rotate the point per the table:
90o counterclock = (-y,x), so (2,2) becomes (-2,2)
- Translate back: (-2,2) + (1,1) = (-2+1,2+1) = (-1,3)
|
|
<==
|
Plot the 3 points (rotation point,
original point and rotated point)
on the above graph.
See if this makes sense.
|
Now, here's a problem for you: Rotate (2,-4) 90o clockwise around (1,-1)
- Subtract (1,-1) from (2,-4) :
- Rotate 90o clockwise: (x,y) = (y,-x) :
- Translate back: add (1,-1) to it :
|
______________
______________
______________
|
|
<== |
Plot the 3 points (rotation point,
original point and rotated point)
on the above graph.
See if this makes sense.
|
|