
Cartesian Coordinates - Reflections about a Line
You are often asked to reflect (or rotate) a point or a polygon about a line. Usually this is either the x-axis, the y-axis or the lines y = x or y = -x. Here are the rules for those reflections:
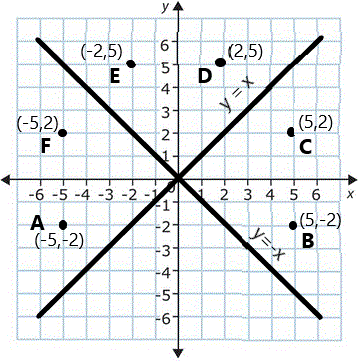
Reflection |
Rule | Example
(see figure)→ |
| About the y-axis |
Negate the x coordinate:
(x,y) → (-x,y) |
Point A → B
(-5,-2) → (5,-2) |
| About the x-axis |
Negate the y coordinate:
(x,y) → (x,-y) |
Point B → C
(5,-2) → (5,2) |
About the line
y = x |
Exchange coordinates:
(x,y) → (y,x) |
Point C → D
(5,2) → (2,5) |
About the line
y = -x |
Exchange and
negate both coordinates:
(x,y) → (-y,-x) |
Point E → F
(-2,5) → (-5,2) |
Suppose you wanted to reflect around a line that is parallel to one of the above 4 defined lines: x-axis, y-axis, y = x or y = -x?
Here's how you do that:
- Compute the translation in either x or y that makes the reflection line cross the origin:
either:
- (dx,0) <== moves the line left or right dx spaces or
- (0,dy) <== moves the line up or down dy spaces.
- Translate the point(s) by this same translation
- Reflect the translated point(s) as shown in the table above
- Translate back to the original position by either:
- (-dx,0) <== if you translated the line in x or
- (0,-dy) <== if you translated the line in y
|
Here's an example:
Reflect (2,2) around the line y = x + 5,
- Compute the translation: The translation you would use is (0,-5)
(this makes the line y = x which goes through the origin)
- Translate the point:
(2,2) + (0,-5) = (2,-3)
- Reflect the translated point:
(2,-3) becomes (-3,2)
(See the above table).
- Translate back:
The opposite of (0,-5) is (0,+5):
(-3,2) + (0,+5) = (-3,7) Get it?
|
Now, here are some of problems for you:
1). Reflect point A about y = x (-5,-2) → (___,___) Plot this point on the grid.
|
2). Reflect point B about y = - x (5,-2) → (___,___) Plot this point on the grid.
|
|
3). Reflect point D about y = - x (2,5) → (___,___) Plot this point on the grid.
| What did point D become under the reflection about y = - x? ___________
Note: It is possible to reflect points about other lines, even arbitrary lines like y = 2x, but that requires trigonometry, a subject you will learn in high school!
|

