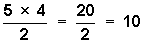Combinations
Combinations are permutations where the order of things doesn't count.
Here's an example:
We have a group of 5 kids:
DAVID BRYAN TONYA BJ CARRIE
We want to form 2-person groups to ride a ferris wheel. How many 2-person
groups can we make? Well, here they are:
<1> <2> <3> <4> <5>
DAVID DAVID DAVID DAVID BRYAN
BRYAN TONYA BJ CARRIE TONYA
<6> <7> <8> <9> <10>
BRYAN BRYAN TONYA TONYA BJ
BJ CARRIE BJ CARRIE CARRIE
Why are there only 10 groups, when the number of permutations of 2 things
out of a set of 5 would be:
5 x 4 = 20?
The reason is that half the permutations (10 of them) are missing! The
missing 10 permutations are:
<1> <2> <3> <4> <5>
BRYAN TONYA BJ CARRIE TONYA
DAVID DAVID DAVID DAVID BRYAN
<6> <7> <8> <9> <10>
BJ CARRIE BJ CARRIE CARRIE
BRYAN BRYAN TONYA TONYA BJ
These are the same as the first 10, but the names are switched.
These don't count, because a 2-person group of BRYAN and DAVID is
the same as DAVID and BRYAN.
So, the number of COMBINATIONS (combinations is the name for
order doesn't count) is:
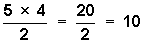Is there a general rule? OF COURSE THERE IS! Here it is:
When choosing 2 where order doesn't count, divide the number of permutations by: 2 (2!)
When choosing 3 where order doesn't count, divide the number of permutations by: 6 (3!)
When choosing N where order doesn't count, divide the number of permutations by: N!
|
|