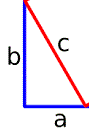
1.) Start with a right triangle
whose sides are a and b
and with hypotenuse c ==>
|
|
|
2.) Make a large square consisting of 4 of the right triangles with an inscribed square whose sides are c in length:
|

|
|
3.) Now, the sides of the larger square are (a + b) in length. The area of this big square is:
|
Big square area = (a + b)2
|
4.) The area of this large square is also the sum of the areas of the 4 right triangles (which is ab/2) plus the area of the inner square, which is c2:
|
Big square area = 4 (ab/2) + c2
|
5.) Since these 2 areas are the same we can set them equal to each other:
|
4 (ab/2) + c2 = (a + b)2
|
6.) By the distributive property:
(a + b)2 = (a + b) (a + b)
= a (a + b) + b ( a + b)
= a2 + ab + ab + b2
= a2 +2ab + b2
| Putting this back in gives us ===>
|
|
4 (ab/2) + c2 = a2 + 2 ab + b2
|
7.) Simplifying the 4(ab/2) term, we have:
|
2ab + c2 = a2 + 2ab + b2
|
8.) Finally, subtracting 2ab from both sides of the equation gives us the theorem of Pythagoras: |
2ab + c2 = a2 + 2ab + b2
-2ab -2ab
|
 Pythagorean theorem proof
Pythagorean theorem proof
 Pythagorean theorem proof
Pythagorean theorem proof