.
|
|
WASHINGTON
STATE MATHEMATICS COUNCIL 2000
MIDDLE SCHOOL MATH OLYMPIAD Session I EIGHTH GRADE
PROBLEM SOLVING |
8 |
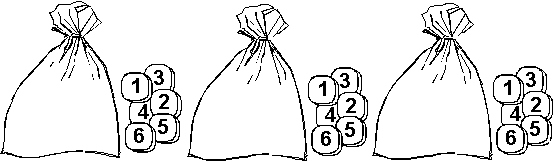
The Tiles Game
Lindsay
has three bags with tiles in them. Each
bag has six tiles in it which are numbered 1, 2, 3, 4, 5, and 6, as shown
below. Lindsay reaches into each bag
and randomly draws out three tiles.
Lindsay adds up the two largest numbers. So, for instance, if she drew tiles that
were 4, 3, and 2, she would add up the 4 and 3 to get 7. If she drew tiles that were 4, 2, and 2, she
would add up the 4 and 2 to get 6.
The problem is to figure out what the
probability is of getting a 7 in this
kind of game, in which you add the top two of three tiles drawn.
Show us your
work. The people who read your paper
are looking at:
- YOUR ANSWER
- YOUR UNDERSTANDING OF THE PROBLEM
Do you understand what the problem is asking? What did you notice about patterns?How did that help you solve the problem? - HOW YOU COMMUNICATE:
Is your reasoning about the problem and about your strategies clearly communicated -- using words, pictures, tables, symbols? - YOUR REASONABLENESS CHECK:
How did you check that your answer was reasonable?
