WASHINGTON STATE MATHEMATICS COUNCIL - 1997 MIDDLE SCHOOL MATH OLYMPIAD
7TH GRADE PROBABILITY & STATISTICS - SCHOOL ___________________________ TEAM_______
1. Out of a bag with 10 colored cubes we drew 10 times, but each time we drew one out, we replaced it before we drew again. After 10 drawings we counted 4 red (R) cubes and 6 green (G) cubes. On the second round of 10 draws there were 3 R and 7 G. The third round had 5 R and 5 G. The 4th round saw 3 R and 7G. The 5th round of 10 had 5 R and 5 G. The 6th round showed 1 R and 9 G. The last round was 7 R and 3 G. Mathematically, the probability shown through the draws matched the 10 cubes. How many red cubes are there out of the 10 cubes?
Answer: ________________
2. A gum-ball machine contains nine red, seven white, and eight green gum balls. What is the least amount of gum balls that a person needs to buy in order to be sure that they get four of the same color?
Answer: ________________
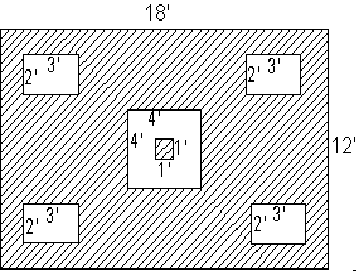
3. The pictured field has shaded and unshaded regions. A helicopter hovers over the field and drops a water balloon. What is the probability that the balloon will land in the shaded area? Express your answer as a fraction in simplest form.
Answer: ________________
4. Consider the game board shown below. Each turn consists of the following steps:
(a) Flip a fair coin
(b) Move two squares to the right for heads, one square to the right for tails
(c) Follow any instructions given on the board.
What is the probability that you will land exactly on square 5 in three turns?
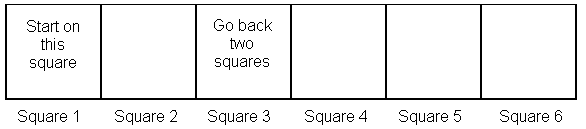
Answer: ________________
5. The ordered list of numbers 18, 21, 24, a, 36, 37, b has a median of 34 and a mean of 35. What is the difference between a and b?
Answer: ________________