Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2006 Grade 5 Geometry
Problem
Solution
1) Each smaller square is made by joining the midpoints of the sides of the larger surrounding square. What fraction of the area of the square ABCD is shaded? Give your answer as a reduced fraction. 1. The triangle in corner "A" has an area of
    1/2 x 1/2 x 1/2 = 1/8th of the square.
2. 4 of these make 1/2 of the square.
3. Take it from here.
    The next inscribed square is 1/2 of the previous one,
4. Doing this 3 times gives the area of
    1/2 x 1/2 x 1/2 = 1/8th of the big square.
5. Fraction shaded = 1/8.
2) An 8-inch square of thin paper is folded in half vertically and then horizontally to create a new square. These 2 folds are repeated 5 times each, including the first two folds, to create a tiny square. What is the perimeter of the new square? (An 8-inch square is a square that is 8 inches on each side.) 1. Each fold halves the area of the square and there are 5 of these folds, so the final area is
    1/2 x 1/2 x 1/2 x 1/2 x 1/2 = 1/32 of the original paper's area.
2. Compute the side length of the folded paper =
    8 x 1/32 = 1/4 inch.
3. Compute the perimeter of the small resulting square =
    1/4 x 4 = 1 inch
3) The figure is missing a measurement for one line segment. What is the missing measurement?
 You don't need any help for this one! ? = 5 cm.

Problem
Solution
4) William cut a rectangle with a perimeter of 36 inches into 2-inch squares with no leftover scraps. What are possible dimensions for William's rectangle? List 3 sets of dimensions giving the length and width. (Note: A rectangle of 2 by 3 inches is the same as a rectangle of 3 by 2 inches.) 1. For a 2-inch square to fit evenly into the rectangle with no gaps or overlaps each dimension of the rectangle must be even.
2. List the dimensions that fit this requirement:
    2 x 16
    4 x 14
    6 x 12 or
    8 x 10. Any 3 of these
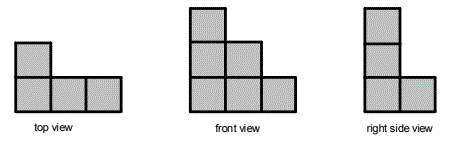
5) A cube sculpture is created from cubes stacked on top of each other and next to each other. Cubes that are stacked meet along their square faces. The top view, front view, and side view of a cube sculpture are given below, where only the squares directly facing you from each view point are shown. What is the least number of cubes you would need to add to the sculpture to make it a solid rectangular prism of cubes?
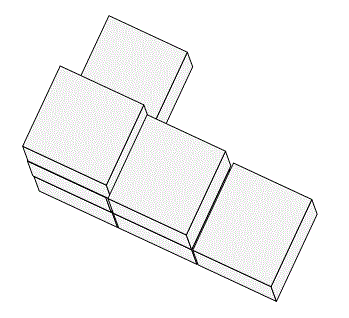1. Figure out the number of cubes in the figure, noting that everything is in the front except for 1 cube. # cubes in the figure = 7.
2. Since the front is 3 across and (by the right side figure) only 2 deep, a solid rectangular prism would have
    3 x 3 x 2 = 18 cubes.
3. Subtract these two to get what you need to add =
    18 - 7 = 11 cubes.
The figure to the right is what this stack looks like.