| Problem |
Hint |
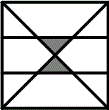1) A dart hits the dartboard shown at random. The board is a square and
the horizontal lines are equally spaced. Find the probability of the dart
landing in the shaded region.
|
You need to find the total area of the two shaded areas.
Use 1 for the square side length.
1. The horizontal lines divide the square into 3 equal rectangles so the height of each rectangle is ____.
2. Since the height of one of those little shaded triangles is half the height of a rectangle, their height ("H") is _____
3. The little unshaded triangles in the upper right and left corners have vertical sides of length = ____.
4. Because the top angle of the triangle is 45o the horizontal side of those little triangles is also _____.
5. That means the base ("B") of one shaded triangle is also _____.
6. Compute the area of one shaded triangle:
A = (B x H) / 2 = _____.
7. Multiply this by 2 to get the
probability of a dart hitting a shaded area = _______
|
|
2) Jesse makes 50% of his free throws and 10% of his half court shots in basketball. What are the
chances that Jesse can make three free throws and a half court shot one right after the other?
|
Multiply the probabilities of 3 free throws and one half court shot together (4 numbers) to get __________.
|
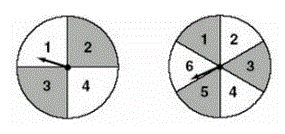
3) In a certain carnival game, a player gets to spin
each of these spinners once. What is the
probability (express as a fraction in lowest terms)
of getting two numbers that have a sum of 7?
|
Fill out this table of sums and find the ones that have a sum of 7, then divide by the total number of sums:
The probability of getting a sum of 7 is _____
|
