| Problem |
Solution |
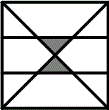1) A dart hits the dartboard shown at random. The board is a square and the horizontal lines are equally spaced. Find the probability of the dart landing in the shaded region.
|
You need to find the total area of the two shaded areas.
Use 1 for the square side length
- The large lower triangle and the shaded triangle that is inside of it are similar because they have parallel bases.
- The height of the large triangle is .5 and the height of the included triangle is 1⁄2 x 1⁄3 = 1⁄6
- Therefore the ratio of their side lengths is 1⁄2 ÷ 1⁄6 = 3
- The base of the small triangle is, therefore, 1⁄3
- The area of the 2 small shaded triangles and the probability of the dart hitting them) is
1⁄3 x 1⁄6 = 1⁄18
|
|
2) Jesse makes 50% of his free throws and 10% of his half court shots in basketball. What are the
chances that Jesse can make three free throws and a half court shot one right after the other?
|
Multiply the probabilities of 3 free throws and one half court shot together (4 numbers):
1/2 x 1/2 x 1/2 x 1/10 = 1/8 x 1/10 = 1/80
|
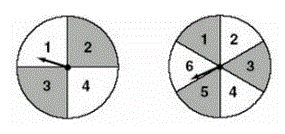
3) In a certain carnival game, a player gets to spin
each of these spinners once. What is the
probability (express as a fraction in lowest terms)
of getting two numbers that have a sum of 7?
|
Fill out this table of sums and find the ones that have a sum of 7, then divide by the total number of sums:
| + |
1 |
2 |
3 |
4 |
5 |
6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
There are 4 of them in the above table.
The probability of getting a sum of 7 is 4/24 = 1/6
|
