| Problem |
Solution |
|
1) Jane bought a 36 inch rope of licorice to share with her brother Andy. She gave Andy a piece
that is three inches more than half the length of her piece. How long is Andy's piece of licorice? |
Let J = length of Jane's piece.
1. Then the expression for Andy's piece is
"3 inches more than half of Jane's piece" = J/2 + 3.
2. Make an equation that adds Jane's and Andy's pieces and sets them equal to the whole length =
J + (J/2 + 3) = 36.
(3/2)J = 33
3J = 66
J = 22
3. Solve for Andy's piece =
(22/2) + 3 = 11 + 3 = 14 inches
|
2) Mr. Jones takes three taxi cab rides with the same cab driver. The table shows how many miles
he traveled and what the taxi fare was. Use the information
to decide what the base fare without tip is for a trip that is 6 miles long.

|
1. Take the difference between the 4 and 2 mile trips and divide by the distance difference = ($14.50 - $8.50)/2 = $3. This is the charge/mile over the base amount.
2. Using the 4 mile trip, subtract the charge/mile to get the base =
$8.50 - 2 X $3 = $2.50.
3. Apply this to the 6 mile trip =
$2.50 + 6 x $3 = $20.50
|
3) Pictured is a sequence of growing chairs. The first chair is made of 6 squares. How squares are in the 20th chair in the sequence?
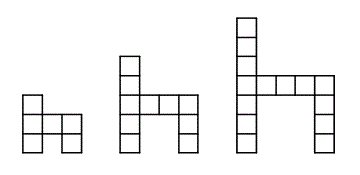
|
1. Write out the sequence of numbers of squares in each chair:
6 10 14 ...
2. Determine the increase in the number of squares per chair = 4 cubes.
3. Use the formula for the Nth term of an arithmetic sequence to determine the number of squares in the 20th chair =
An = A1 + D (n - 1) where:
An = Nth term (the term you are looking for)
A1 = First term
D = Number added to each term
A20 = 6 + 4 (19) = 82 chairs
|