| Problem |
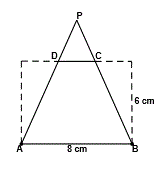3) In the diagram, the length of the rectangle is 8 cm, the width is 6 cm.
The area of isosceles triangle PDC is 4 cm2.
The height of isosceles triangle PAB is 50% greater than the height of trapezoid ABCD.
What is the area of isosceles trapezoid ABCD?
|
| Solution |
There are 3 ways to solve this problem: 2 by area subtraction and one by the formula for the area of a trapezoid.
1. First, determine the height of triangle PAB.
It is 50% greater than the height of ABCD (which is 6 cm.), so it is 9 cm. Call this H1
2. This makes the height of triangle PDC 9 - 6 cm. = 3 cm. Call this H2.
We can use one of three methods to determine the trapezoid area.
Here they are:
Method 1: Area subtraction #1.
1. The idea is to determine the areas the large triangle, PAB, and subtract the area of PDC from it. That leaves the trapezoid!
2. Triangle PAB area =
(8 x H1) / 2 = *8 x 9) / 2 = 36 sq. cm.
3. Triangle PDC area = 4 sq. cm.
4. Subtract the second area from the first to get the area of the trapezoid =
36 - 4 = 32 sq. cm.
|
Method 2: Area subtraction #2.
1. The idea is to determine the area the large rectangle and subtract the areas of the two dotted triangles from it. That leaves the trapezoid!
2. From the area of triangle PDC (4 cm2) you can get the length DC:
Triangle Area = base x height / 2
4 = (H2 x DC) / 2, so
DC = (4 x 2) / 3 = 8/3 cm.
3. Area of the rectangle =
8 x 6 = 48 sq. cm.
4. Base of one dotted triangle =
(8 - 8/3) / 2 = 8/3 cm. .
5. Area of one dotted triangle =
(8/3 x 6) / 2 = 8 sq. cm.
6. Subtract 2 of these from the rectangle =
48 - 16 = 32 sq. cm.
|
Method 3: Area of a trapezoid
1. From the area of triangle PDC
(4 cm2) you can get the length DC:
Triangle Area = base x height / 2
4 = (H2 x DC) / 2, so
DC = (4 x 2) / 3 = 8/3 cm.
2. The area of a trapezoid is
Area = (b1 + b2) H / 2 where:
b1 is the length AB (8 cm.)
b2 is the length DC (8⁄3)
and
H = the height (6 cm.)
3. Area of the trapezoid =
(8 + 8/3) x (6 / 2) =
(32/3) x 3 = 32 sq. cm.
|
|
| Problem |
Solution |
|
4) Quadrilateral ABCD has three congruent sides AB, AD, and DC. It has a right angle at A, an acute angle at D, and an obtuse angle at C. What is the range of values for angle at D for these things to be true?
|
1. So the angle at D must be less than 90 degrees because if it were that angle or greater, then C would be 90o or less.
In the figure, this is angle ADC1
2. It also must be greater than 45 degrees to keep the angle at C obtuse (less than 180o).
In the figure, angle ADC2 shows an angle that results in an angle at C greater than 180o.
|
|
5) Dee has 9 cubes. She wants to build a large cube that takes more than 9 cubes. What is the fewest number of cubes she would need to add to be able to build it?
|
Make a table like this:
Cube side length
(# of small cubes) | Total number of small cubes
in the larger cube |
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
| 4 | 64 |
The first entry that has more than 9 cubes is the one with 3 small cubes on a side, consisting of 27 cubes. Subtract 9 from this number of cubes to get the answer = 27 - 9 = 18 cubes.
|
|
|
