| Problem |
Hint |
1) It costs $50.00 each day to run a small pudding factory. It costs 25 cents to make a pudding cup. How many
pudding cups can be made in that day if the factory has $516.00?
|
Let N = number of pudding cups
Write an equation for N which is
(a) the money the factory has, minus
(b) the cost each day to run the factory, divided by
(c) the cost per cup of pudding:
The equation: N = _________________
Solve for N = _____
|
2) Two ice cream men are racing to the park along the same route. Ice cream man Chandler is going 24
meters per minute. Ice cream man Joey is going 3600 centimeters in one minute. Chandler gets to the park
in 4 minutes. If they started from the same point, how long will it take Joey to get to the park? Express
your answer in minutes and seconds. |
1. Convert Joey's rate to meters/minute = _____
2. Compute the distance Chandler went in 4 minutes = ____ meters.
3. Divide this distance by Joey's rate to get Joey's time = _____ minutes.
4. Convert this to minutes and seconds = ______
|
3) Jordan's backyard is 1300 square feet. She is willing to devote 12% of her yard to a trampoline. What
would be the diameter of the largest circular trampoline that would satisfy that? Circular trampolines only
come in whole number diameters. Use 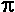 = 3.14 = 3.14 |
1. Compute 12% of the backyard's area = _____ sq. ft.
2. Take the square root of this to find the trampoline's radius = _____ ft.
3. Multiply this by 2 and round down to the next whole foot = _____
|