
|
Washington State Math Olympiad
Hints and Solutions
2011 Grade 5 Algebra
|
 |
| Problem |
|
1) On January 1st Linda has $14 in savings and John has $62. Linda saves $4.50 each month. John notices he spends $3.50 out of savings every month to build his tournament game card collection. On the first of which month will they have the same amount if this pattern continues?
|
| Solution(s) |
There are 3 ways to solve this problem:
Method 1:Write an equation:
1. Let N = number of the month past January that they will have the same amount.
2. Linda's side of the equation must equal Johns, so:
3. Linda's expression:_____________________
4. John's expression:______________________
5. Set them equal to each other and solve:
________________________________
N= ___ Month = _____
|
Method 2:By deductive logic:
1. Every month the difference between Linda's and John's savings decreases by ______
2. The difference between their January savings is
__________
3. Divide this difference by the decrease and you have the number of months until they are equal =
________________(months past January)
4. That month is _______.
|
Method 3:Make a table:
Complete this table to find the month their savings accounts equal:
| Month | Linda's
acct. | John's
acct |
| January | $14 | $62 |
| February | | |
| March | | |
| April | | |
| May | | |
| June | | |
| July | | |
|
|
| Problem |
Solution |
|
2) Jim wants to swim 36 yards out into the ocean from the shore. He swims out 6 yards in 4 seconds but then in one second a wave pushes him back 3 yards. If this cycle continues, how long will it take Jim to get 36 yards out into the ocean from the shore for the first time?
|
Method 1: Make a table:
| Cycle | time
(sec) | Start
(yards) | Swim
out
(yards) | Push
back
(yards) |
| 1 | 0 | 0 | 6 | 3 |
| 2 | 5 | 3 | 9 | 6 |
| | | | | |
| | | | | | | | | | | |
| | | | | |
| | | | | |
| | | | | | | | | | | |
| | | | | |
| | | | | |
| | | | | |
Jim reaches 36 yards at ____ seconds.
|
Method 2: Use analysis:
1. Compute how far Jim progresses after a swim out and then a push back =___ yards.
2. Divide the total distance, 36 yards, by this amount = _____ cycles
3. This means that after ____ full cycles he has progressed 36 yards.
4. On the previous cycle, _____, he went out 36 before he got pushed back 3, so he achieved 36 yards after ____ cycles.
5. It takes _____ seconds for cycle ____, but he didn't get pushed back, so the total time is _____ seconds.
|
|
|
| Problem |
Solution |
3) In the pattern of figures shown below
how many unit squares are needed to build the 8th figure?
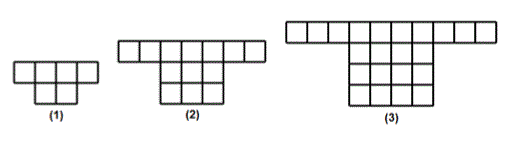
|
OK, this is tricky because there are actually 2 sequences that are added together:
1. The top horizontal top row
2. The blocks below the top row
Method 1:Make a table
Here they are in a table
(N is the figure number):
| N | Top row | bottom
blocks | total |
| 1 | 4 | 2 | 6 |
| 2 | 7 | 6 | 13 |
| 3 | 10 | 12 | 22 |
| 4 | | | |
| 5 | | | |
| 6 | | | |
| 7 | | | |
| 8 | | | |
|
Method 2: Find the equations:
1. Top row: Every figure adds ___ blocks so the top row equation is:
An = A1 + ___(n - 1)
A8 = _______
2. Bottom blocks (B): Every figure contains
N x ____ blocks, so :
B8 = ________ blocks.
3. Add these 2 together:
A8 + B8 =
______ blocks.
|
|
|
| Problem |
Hint |
|
4) Each week, Roxy mows Mrs. Smith's lawn and does some extra yard work. Mrs. Smith pays Roxy a fixed amount for mowing her lawn. He earns an additional hourly amount for extra work. Based on the table below, how much is the hourly amount for the extra work?
|
You only need the first 2 columns to solve this problem.
1. The increase from the first week to the second week is $_____
2. The number of additional hours for extra work in the second week over the first week was _____ hours.
3. That increase divided by the number of additional hours gives you the extra hourly rate = $______
|
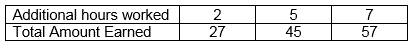 |
5) In the letter puzzle given, each letter stands for a different number from the list 1, 2, 3, 4, 5, 6. The value of O is less than the value of W. What number is WOW?
NET
+TEN
WOW
|
- Only 5 letters are in the sum, so one of the digits 1-6 is not there.
- The second column is E + E so E must be 3 or less or their sum would add to more than 6. So E is 1, 2, or 3.
- If E = 3, then O is 6 which cannot be because it is less than W, so E is either 1 or 2.
- Columns 1 and 3 both add T + N , so they, too, must add to 6 or less.
- Start with the possibilities for E and see if values for O, T and N are possible:
- E = 1; If E is 1 then O is ____ and the possibilities for T and N are:
- E = 2; If E is 2 then O is ____ and the possibilities for T and N are:
With these hints you should be able to find what WOW = ______
|
|
|