Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2012 Grade 6 Geometry
Editor's note: In my opinion, problem #1 is inappropriate for 6th graders. I provide a hint and a (very long) solution, but don't suggest you give this to your students. If you choose to use this problem, cover this comment with a marker.
Problem
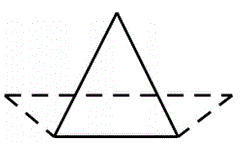1) An isosceles triangle and an isosceles trapezoid share a common base (solid line) and have the same area. However the trapezoid has 1/3 the height of the larger triangle. What fraction of the longer base of the trapezoid extends outside the triangle?

2) A three dimensional object can be represented by different views: looking down from above (top view), looking from the front (front view), and looking from the right (right side view). Each picture only shows what is facing you directly from that view. What is the fewest number of cubes that could be in the grouping described by the three pictures?

3) Six paper cones for cotton candy are created from a circle with radius 6 inches by cutting out pie shaped pieces that each are one sixth of the circle and then taping together their edges. What is the radius of the circular rim of one of the cones if there is no overlapping when the edges are taped?
(Drawing not to scale.)

Problem

4) A regular tetrahedron can be formed from an equilateral triangle by folding along the dotted lines as shown in the figure. Maria is experimenting. The first tetrahedron she folds looks too small to her. She scales it up by doubling the edge lengths. What is the ratio of the surface area of the bigger tetrahedron to the original tetrahedron?

5) The base of an isosceles triangle has vertices at (1,1) and (5,5) as shown. Its height is 3/4 the length of its base. What can the coordinates of its vertex be?