Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2012 Grade 6 Geometry
Problem
Hint
1) An isosceles triangle and an isosceles trapezoid share a common base (solid line) and have the same area. However the trapezoid has 1/3 the height of the larger triangle. What fraction of the longer base of the trapezoid extends outside the triangle?
 Let B = length of the common base and
    Bt = length of the trapezoid's second base.
  1. The formula for the area of a triangle is   (B H) / 2
  2. The formula for the area of the trapezoid is (B + Bt) H / 2
  3. Set these two areas equal to each other
    and solve for Bt


    = _____
  4. The 2 triangles are similar because the second base is parallel to the first, so their bases are in the same ratio as their heights. The length of the (smaller) second base, in terms of the big triangle's base is


    __________
  5. Subtract this length from the length of the long trapezoid base you got (above) to get the length that is outside the triangle =


    = ____________
  6. Now, divide this length by the total length of the second base to get the ratio =


    ____________
2) A three dimensional object can be represented by different views: looking down from above (top view), looking from the front (front view), and looking from the right (right side view). Each picture only shows what is facing you directly from that view. What is the fewest number of cubes that could be in the grouping described by the three pictures? 1. From the right side view, there are at least ___ cubes in the figure.
2. From the front view there are at least ____ more that are not shown in the right side view.
3. There are none shown in the top view that are not accounted for in the other 2 views,
therefore the minimum number of cubes is ____

Problem
Hint
3) Six paper cones for cotton candy are created from a circle with radius 6 inches by cutting out pie shaped pieces that each are one sixth of the circle and then taping together their edges. What is the radius of the circular rim of one of the cones if there is no overlapping when the edges are taped?
(Drawing not to scale.)		 1. Compute the circumference of the circle:
    C = _______
2. Divide that by 6 = ______.
This is the circumference of the base of the cone
3. Compute the radius of the base of the cone, given this circumference: R = _____

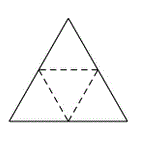4) A regular tetrahedron can be formed from an equilateral triangle by folding along the dotted lines as shown in the figure. Maria is experimenting. The first tetrahedron she folds looks too small to her. She scales it up by doubling the edge lengths. What is the ratio of the surface area of the bigger tetrahedron to the original tetrahedron?		 The fact that the equilateral triangle can be folded into a tetrahedron is irrelevant to this problem! Also, the fact that the triangle is equilateral is irrelevant, too!
1. Here is the area of the original triangle :
    A = (B H) / 2
2. Write the the equation for the area of a triangle whose base and height are twice as big:
    Abig = _______________
3. Divide this by the original triangle area:
4. Ratio = __________
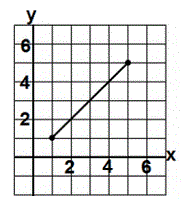5) The base of an isosceles triangle has vertices at (1,1) and (5,5) as shown. Its height is 3/4 the length of its base. What can the coordinates of its vertex be?
 Solve by inspection:
1. Calling the length of one little 1x1 square diagonals D, the length of the base is ____ x D.
2. 3/4ths of this is _____ diagonals D
3. Find the midpoint of the base: = (___,___)
4. From this point move perpendicular to the base, both right and left from the base the above number of diagonals to get the 2 points.
    Put a dot on each of these 2 points.
5. These 2 points are (___,___) and (___,___).