Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2012 Grade 6 Geometry
Problem
Solution
1) An isosceles triangle and an isosceles trapezoid share a common base (solid line) and have the same area. However the trapezoid has 1/3 the height of the larger triangle. What fraction of the longer base of the trapezoid extends outside the triangle?
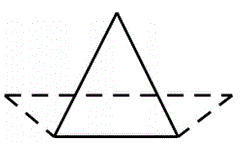
Let B = length of the common base and
    Bt = length of the trapezoid's second base. (the long one)
    H = the triangle's height and
    Ht = the trapezoid's height = H/3
  1. The formula for the area of a triangle is       (B H) / 2
  2. The formula for the area of the trapezoid is
        (B + Bt) Ht / 2
  3. Set these two areas equal to each other and solve for Bt =
    BH/2 = (B+Bt) (H/3)/2
    BH = (B+Bt) H/3
    B = (B+Bt)/3
    3B = B + Bt
    2B = Bt therefore
    Bt = 2B.
    In other words, the second base of the trapezoid (Bt) is twice the length of the other base (B).
  4. The 2 triangles are similar, so the length of the second base that is inside the triangle is 2⁄3 B because it's height is 2⁄3 of the big triangle's height.
  5. The portion that is outside the base is
    2B - 2⁄3B = 4⁄3B
  6. The fraction of the long trapezoid base that is outside the triangle is 4⁄3B / 2B = 2⁄3
So, this means the longer base of the trapezoid, which is twice the length of the other base, B, is cut into 3 equal parts, each of which is 2⁄3B in length, so 2 of those 3 equal parts are outside the triangle!

Problem
Solution
2) A three dimensional object can be represented by different views: looking down from above (top view), looking from the front (front view), and looking from the right (right side view). Each picture only shows what is facing you directly from that view. What is the fewest number of cubes that could be in the grouping described by the three pictures? 1. From the right side view, there are at least 7 cubes in the figure.
2. From the front view there are at least 2 more that are not shown in the right side view.
3. There are none shown in the top view that are not accounted for in the other 2 views,
therefore the minimum number of cubes is 9

3) Six paper cones for cotton candy are created from a circle with radius 6 inches by cutting out pie shaped pieces that each are one sixth of the circle and then taping together their edges. What is the radius of the circular rim of one of the cones if there is no overlapping when the edges are taped?
(Drawing not to scale.)		 1. Compute the circumference of the circle:
    C = 12
2. Divide that by 6 = 2 .
This is the circumference of the base of the cone
3. Compute the radius of the base of the cone, given this circumference: 2R = 2
4. R = 1

Problem
Solution
4) A regular tetrahedron can be formed from an equilateral triangle by folding along the dotted lines as shown in the figure. Maria is experimenting. The first tetrahedron she folds looks too small to her. She scales it up by doubling the edge lengths. What is the ratio of the surface area of the bigger tetrahedron to the original tetrahedron? The fact that the equilateral triangle can be folded into a tetrahedron is irrelevant to this problem! Also, the fact that the triangle is equilateral is irrelevant, too!
1. Here is the area of the original triangle :
    A = (B H) / 2
2. Write the the equation for the area of a triangle whose base and height are twice as big:
    Abig = (2B x 2H)/2
3. Divide this by the original triangle area:
    (2B x 2H)/2 / BH/2 = 4BH/BH = 4.
4. Ratio = 4

5) The base of an isosceles triangle has vertices at (1,1) and (5,5) as shown. Its height is 3/4 the length of its base. What can the coordinates of its vertex be?
 Solve by inspection:
1. Calling the diagonal length of one little 1x1 square D,
    the length of the base is 4D
2. 3/4ths of this is 3 diagonals, 3D
3. Find the midpoint of the base: = (+3,+3)
4. From this point move perpendicular (at a 45 degree angle) both right and left from the base 3 diagonals (3D) to get the 2 points.
    Put a dot on each of these 2 points.
5. These 2 points are (+6,0) and (0,+6).

See the figure to the left.