| Problem |
Hint |
|
1) Rectangle A and rectangle B both have area 72 sq.cm. The lengths and widths of both rectangles are integers. The width of rectangle B is 5 cm greater than the width of rectangle A. The length of rectangle B is 15 cm less than the length of rectangle A. Which rectangle has the greater perimeter and how much greater is it? |
Let L1 = length of rectangle A
W1 = width of rectangle A
L2 = length of rectangle B
W2 = width of rectangle B
1. The perimeter of rectangle A is ______________
2. The perimeter of rectangle B is ______________
3. From this information you should be able to figure out which rectangle has the greater perimeter and by how much:
_________________________
|
|
2) Mr. Clear likes cutting things. He has a piece of paper 1/400th of an inch thick, which he cuts in half and stacks on top of the other half. Mr. Clear cuts and stacks a total of 15
times. How tall is the stack of paper now? Express your answer in feet and inches rounded to the nearest whole number. |
It helps if you have a calculator that can do exponents.
If you do, compute 215 = _____
If you don't, multiply 2 by itself 15 times = _____
Divide 215 by 400 = ______________
|
3) At Pizza-R-Us, you can buy a circular pizza with a diameter of 14 inches or a square pizza with 13 inch side lengths. For both pizzas, the baker pours sauce on the entire pizza except for a 1 inch border around the edges. What is the difference in areas between the sauce covered regions of the two pizzas? Express your answer to the nearest square inch.
You may use 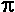 = 3.14 = 3.14 |
1. Take 2 inches off each dimension and compute the areas of the two pizzas:
Round: _____
Square: _____
2. Take the difference between these two areas =
_____ rounds to _____
|