| Problem |
Hint |
|
1) The distance around a track is 1/4 mile. Jessie plans to run 5 miles and has already done 6 laps.
How many more laps must she run to complete 5 miles?
|
1. Compute the number of laps in 5 miles = _____ laps.
2. Subtract the laps she has already done.
Remaining = _____ laps.
|
2) At the end of February Jenny noticed that she could finally get up when it was light in the
morning. She kept track of when sunrise was for a few days in the paper and saw a pattern:
| Feb 24, 2013 | 6:59 AM |
| Feb 25, 2013 | 6:57 AM |
| Feb 26, 2013 | 6:55 AM |
| Feb 27, 2013 | 6:53 AM |
If the pattern holds true, when was sunrise on February 1st? |
1. Find the amount of time the sunrise advances for 1 day = _____ min.
2. Compute the number of days from Feb 1st to the 24th = ____ days.
Remember, don't count the 24th!
3. Multiply this by the number of minutes the time advances in one 1 day
= ____ minutes.
4. Compute the time of sunrise on the 1st, going back this number of minutes = _____ am.
|
3) The figure shows a sequence of castle
fronts made from cubes. The number of
cubes needed for each castle front form a
numerical pattern. How many cubes are
needed for the castle front of Castle 8?
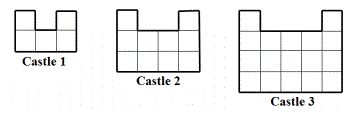
|
1. This is actually 2 sequences added together.
2. The first sequence is the number of cubes on the top of each castle (a constant) = ___ cubes.
3. The second sequence is the number of cubes making the remainder of the castle front. Write out that sequence =
4. For each castle, N, then this second sequence is N x (_____).
5. Compute the number of cubes in the 8th castle as the number of cubes in the first sequence + the number of cubes in the remainder, using N = 8 =
_____ total cubes.
|