1) Lamar wants a circular pool in his back yard. He maps out the circle and decides it is far too small. If Lamar increases the diameter by 6 feet, it doubles the circumference. What is the
circumference of the bigger circle?
You may leave your answer in terms of 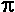
or use 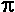 = 3.14 and round to the nearest tenth. = 3.14 and round to the nearest tenth.
|
1. If you increase the circumference of a circle by a factor of X, then the diameter is increased by that same factor.
2. Compute the diameter of the original pool = 6 ft.
3. Compute the diameter of the larger pool = 12 ft.
4. Compute the circumference of the larger pool =
12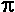 or 37.7 sq. ft or 37.7 sq. ft
|
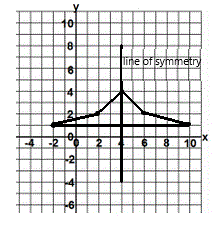
2) Some of the vertices of a polygon are located at the
coordinates
(-2, 1), (2, 2), and (4, 4). The polygon has a
vertical line of symmetry at x = 4 which meets the opposite
edge at the midpoint (4, 1). Name the polygon that has the
fewest number of vertices satisfying these conditions, and
give the coordinates for one its other vertices.
|
First, this is not a regular polygon.
1. The fact that the line of symmetry goes through one of the points means the polygon has an odd number of points (the one on the line is not replicated, but the other 2 are). This means the polygon has at least 5 sides and is a pentagon.
2. From the line of symmetry, find the two points that mirror-image the other 2 given points.
They are (10,1) and (6,2).
The figure to the left shows this pentagon and its line of symmetry.
|