|
4) Ms. Schultz passes out strawberries to her Spanish class. If she gives each student 6 strawberries,
she has 28 left. If she gives each student 8 strawberries, she has 4 left. How many strawberries does
Ms. Schultz have? |
1. Subtract the number left from passing out 8 strawberries from the number left after passing out 6 =
28 - 4 = 24 strawberries.
2. These were shared by 2 students so there are 12 students in her class.
3. Multiply this number of students by 8 and add 4 to get the total number of strawberries =
12 x 8 + 4 = 100.
4. Check this with the computation for 6 students:
12 x 6 + 28 = 72 + 28 = 100. It checks!
|
5) In the pattern of circles shown, each new encircling layer adds more circles. The layers alternate in color beginning with white, then grey, and then white. When the pattern has exactly 3 grey layers, how many circles of both colors are in the pattern?
|
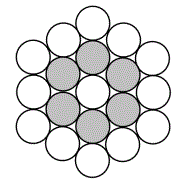
Method 1: Analyze the layering.
The figure has 6 sides and with each additional layer still has 6 sides.
1. Each layer adds 1 to the length of a side,
so the next gray layer has sides that are 4 circles long
and the next white layer has sides that are 5 circles long.
and the last gray layer has sides that are 6 circles long.
2. But the circles on the corners are shared by the adjacent sides, so
6 of them must be subtracted from each layer.
3. The next gray layer has 4 X 6 - 6 shared circles, leaving 18 circles.
4. The next white layer has 5 X 6 - 6 shared circles, leaving 24 circles.
5. The next gray layer has 6 X 6 - 6 shared circles, leaving 30 circles..
6. Adding these up gives us a total of
1 + 6 + 12 + 18 + 24 + 30 = 91 circles in the figure.
Method 2: Use the formula for the sum of an arithmetic sequence:
1. Write down the number of circles in each layer:
1 6 12 ...
2. Ignoring the one in the center, each layer adds 6 circles.
3. When the pattern has 3 grey circles it will have a total of 5 layers (ignoring the one in the middle).
4. The 5th term of this sequence is A5 = 6 + 6 (5 - 1) = 30
5. The formula for the sum of an arithmetic sequence is:
Sum = ((A1 + An) x n) / 2
6. So the sum is (6 + 30) x 5 / 2 = 18 x 5 = 90.
7. Add the one in the center and the total is 91.
|
3) Maya loves dogs and is happy to dog sit for her neighbors.
She charges a small initial fee and then an hourly rate. Based
on the table, what is an expression that will let her quickly
compute how much she will earn for h hours of dog sitting for
one dog?