Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2014 Grade 6 Probability & Statistics
Problem
Solution
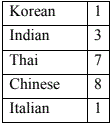1) Restaurants often slip takeout menus under Rudy's apartment door. Rudy made a chart of how many menus were from each kind of restaurant. If this data is representative, then how many of the next 15 menus slipped under Rudy's apartment door will be Chinese? 1. The total number of menus Rudy received was 20.
2. Compute the fraction of the menus that are Chinese = 8/20 = 2/5
3. Apply this fraction to the next 15 menus = 2/5 x 15 =
    6 menus.

2) The 6th grade classes at Benge Elementary completed a final science test. The average score of the female students is 82 and the average score of the male students is 79. There are 42 girls and 38 boys in the 6th grade. What is the average test score of the entire sixth grade to the nearest whole number?		 1. Multiply the girls' average by the number of girls =
    82 x 42 = 3444
2. Multiply the boys' average times the number of boys =
    79 x 38 = 3002
3. Add these 2 numbers and divide by the total number of students. =
    (3444 + 3002)/(42 + 38) = 6446/80 = 80.575
4. Class average (rounded) is 81

3) A target includes 5 concentric circles with diameters of 2, 3, 4, 5, and 6 inches. Assume Jody always hits the target but it is random where on the board the dart hits. What is the probability that she hits the area between the 4 inch and 6 inch diameter circles? Express your answer as a percentage to the nearest tenth.		 1. The target area between the 4 inch and 6 inch diameters are the 6 and 5 inch diameter circles.
2. Compute the area of the 6 in. diameteter circle =
    3.14 x 32 = 28.26 sq. in.
3. Subtract the area of the 4 in. diameter circle =
    3.14 x 4 = 12.56
4. 28.26 - 12.56 = 15.7 sq. in.
5. The probability = 15.7/28.26 = .5555 rounded = 55.6%

Problem
Solution
4) When rolling a single six sided die three times, how much more likely are you to roll all three different numbers compared to all three the same number? Express your answer as a ratio. You roll the first die to get a number.
Probability of all 3 being different:
1. The probability of the second die having a different number is 5/6
2. Assuming that second number was different than the first one what is the probability of the third die not matching the either of those 2? 4/6
3. Multiply these 2 probabilities together to get the probability of all 3 rolls being different =
    5/6 x 2/3 = 10/18 =5/9
Probability of all dice being the same:
4. Back to that second die.
    What is the probability that it matched the first die? 1/6
5. For the third die, what is the probability that it matches the first 2? 1/6
6. Multiply these 2 together to get the probability of both rolls matching the first = 1/6 x 1/6 = 1/36
Ratio of these 2 possibilities:
7. Divide the result of step 3 by the result of step 6 =
    (5/9) / (1/36) = (5 x 4) = 20. The ratio is 20:1
5) There are 25 students in Mr. B.'s class. Tori is one of the students who has a $2.00 weekly allowance. Which value, mean or median, should she report to her parents to persuade them to give her a higher allowance? Write your choice and its value.
 1. Compute the mean of the 25 allowances =
    3 x 0 + 5 x 2 + 2 x 2.25 + 4 x 2.5 +
    4 x 3.5 + 2 x 3.75 + 3 x 4 + 1 x 5 + 1 x 7.5 =
    70.5/25 = $2.82
2. In an ordered list (which this is) the median is the middle one, which for a class of 25 is the 13th allowance, counting from either the left or right.
That allowance is $2.50
3. She should take the lower of the 2 = $2.50
and report the median to her parents.