| Problem |
Hint |
1) Determine the total number of squares in this figure. |
There are squares of 4 different sizes:
l.In terms of small squares:
4x4, 3x3, 2x2, and 1 small square.
2. Count up the number of squares of each size and add = ____
|
2) A rectangular wooden box measuring 3 in x 5 in x 7 in is immersed in black paint and then cut into 1 in cubes. What fraction of the resulting cubes will have no paint on any of the faces?
|
1. Each dimension will be reduced by 2 to count the number of no-paint cubes.
2. Subtract 2 from each dimension and multiply =
_____ cubes.
3. Total cubes = _____.
4. Fraction = _____
|
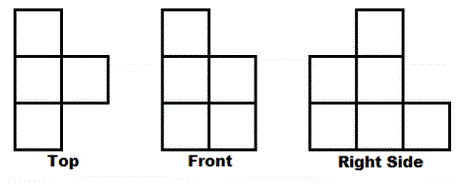
3) A three-dimensional
object can be represented
by different perspectives:
from above (Top view),
from the front (Front
view), and from the side
(typically, Right Side
view). This figure shows
you an arrangement of
cubes. What is the
greatest number of cubes
that could be in the
arrangement shown?
|
This figure numbers the cube faces for the following discussion:
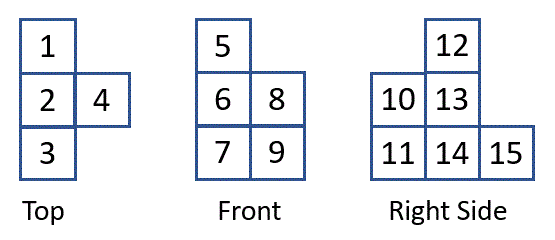1. Here are faces that are faces of the same cubes:
- 1 & 15 (a cube by itself)
- 2 & 12 (making this the top of a 3-cube stack)
- 3 & 10 (making this the top of a 2-cube stack)
- 8 & 13 (making this the top of a 2-cube stack)
2. Put the size of these stacks on the "top" figure.
3. The number of cubes is _____
|
