Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2016 Grade 6 Geometry
Problem
Hint
1) A square can be split to make four smaller squares of equal sizes to completely fill the original square as shown. How would you split up the original square into six smaller squares that completely fill the original square without any overlaps of the smaller squares?
(The squares do not all need to be the same size.) 		1. Cut the square into 9 equal sized smaller ones.
2. You should be able to solve this once you look at this diagram by combining these smaller squares.
Use this square:

2) If the total surface area of a cube is 150 sq. cm., what is its volume?


 1. The surface area consists of 6 of the faces.
2. Set this equal to 150 and solve for the length of a side: = ____
3. Compute the volume as the side length cubed = _____

Problem
Hint
3) In rectangle ABCD, X is the midpoint of CD and Y is the midpoint of AD. What percentage of the figure does the shaded area represent?


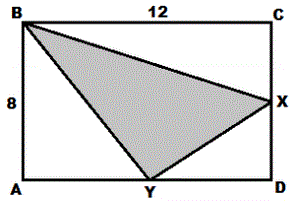
 1. Put the lengths of the sides XC, XD, AY and YD on the figure.
2. Compute the area of the 3 non-shaded triangles and subtract their sum from the area of the rectangle = ____
3. Divide this by the area of the rectangle = _____
4) What is the sum of all the interior angles of an octagon?

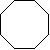
 Method 1: Use analysis
Use this figure on the left to analyze this problem:
1. Put a dot in the center and draw lines from this dot to each vertex of the octagon. This makes 8 triangles with a common vertex in the center of the octagon.
2.Compute the center vertex angle of one triangle as 1/8 of a circle (because they all add to 360o) = _____ degrees.
3. The other 2 angles of each of the triangles add to _____ degrees.
4. The interior angle of the octagon consists of 2 of these other angles, so the interior angle of a single octagon vertex = _____.
5. Multiply this by the number of vertices = _____ degrees.

Method 2: Use the interior angles of a polygon formula:
1. The sum of the angles of a polygon is 180 ( n - 2)
    where n = number of sides.
2. Solve this for n = 8:
    S = ______
5) How long is segment BC?
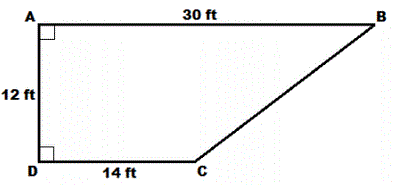
 1. Draw a line from point c to line AB parallel to AD.
2. This forms a triangle. Label it's sides from other information in the diagram.
The 2 sides of the triangle are _____ and _____ feet.

Method 1: Use the Pythagorean theorem
compute the length of BC = _____

Method 2: Examine the triangle
1. Find the common factor of the 2 given sides. Factor = ____
2. Divide both measurements by this factor:
  Sides = _____ and _____.
3. You should notice something about these measurements that lead you directly to the length of the other side
  =   ______ feet. Put the scale factor back in and you get
_____ feet.