Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2017 Grade 6 Algebra
Problem
Solution
1) Parmveer has a bag with 54 coins. Altogether the coins are worth $4.75. He only has nickels and dimes in the bag. How many dimes are in the bag?
Method 1: guess-and-check.
# nickels#dimesTotal
1341$4.10
 Method 2: Use 2 equations.
Use N for the number of nickels and
    D for the number of dimes.
1. The equation for the number of coins:
    N + D = 54
2. The equation for the sum of the coins:
    5N + 10D = 475
3. Write an expression for N using the first equation and then substitute it in the second equation and solve.
    N = 54 - D
    5(54 - D) + 10D = 475
    270 - 5D + 10D = 475
    5D = 205, so     D = 41
2) Evaluate:
    8x2 - (4x - 17) if 4x - 11 = 3		 1. Rewrite the second expression as x = something
    4x = 14
    x = 3.5
2. Substitute it in the first equation.
    8(3.5)2 - 4(3.5) + 17
    98 - 14 + 17 = 101
3) Shalem started with a certain amount of money. Every day he spends the same amount. After the 4th day he has $117 left. After the 36th day he has $13 left.
    a. How much money did he start with?
    b. How much does he spend each day?		 1. Subtract the amount he had after the 36th day from the amount he had after the 4th day and divide by the number of days between them =
    (117 - 13)/32 = $3.25/day
2. Add 4 times the daily amount to get the amount he started with =
    $117 + 4 X $3.25 = $130

Problem
Solution
4) In Josie's class there are 28 students. 13 have been to Oregon, 11 have been to Idaho, and 3 have been to both. How many students have not been to either Oregon or Idaho? Method 1: Use a Venn diagram
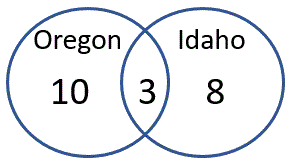Your Venn diagram should look like this:
1. Draw the numbers in the diagram and then add the 3 components = 10 + 3 + 8 = 21 students have been to Oregon, Idaho or both.
2. Subtract this from 28 - 21 = 7 students.

Method 2: Use logic:
1. If 13 students have been to Oregon and 3 of those also have been to Idaho, then 10 have been to Oregon only.
2. If 11 students have been to Idaho and 3 of those also have been to Oregon, then 8 have been to Idaho only.
3. Add these two to the number that have been to both =
    10 + 8 + 3 = 21 students
4. Subtract this from the total: 28 = 21 = 7 students.
5) I'm thinking of a positive number. If I square it and then subtract 65, I get the same answer as when I multiply my number by 8. What is my number? Use x for your number.
1. Write an expression for "square it and subtract 65" =
    x2 - 65
2. Write an expression for "multiply my number by 8" =
    8x
3. Set these equal to each other and solve.
    x2 -65 = 8x
    x2 - 8x - 65 = 0.
    Use the quadratic formula: (constants: a = 1, b = -8, c = -65)
    x = 8 ± √ 8 2 - (4) (1) (-65)     
                  2
    x = 8 ± √ 64 +260      So:
                  2
    x = 8 ± 18     x = 4 + 9 = 13
            2
Note: x = -5 is also a solution to this equation, but the problem asked for a positive number!