| Problem |
Solution |
|
1) A cube has the same numeric value for its surface area and its volume. How many units is its side
length?
|
Use s for the length of the cube's side.
1. The surface area of a cube is 6 times the square of the side length.
2. The volume of the cube is the side length cubed.
3. Write an equation setting these 2 things equal to each other and solve for the side length s
6s2 = s3
divide both sides by s2
6s2 = s3 s = 6
s2 s2
|
2) JIHG is a square with an area of 36 square inches.
JN is 1/3 of JI.
What is the area of square KNML?
|
1. Compute the side lengths of the large square =
√
36 = 6 in.
2. If KNML is a square, then all the triangles
JNK, NIM, KGL and LHM are congruent (they are identical).
3. All the triangles have a short side JN = 6 x (1/3) = 2
and a long side NI = 6 - 2 = 4
4. Find the area of one of the triangles = (2 x 4)/2 = 4 sq. in.
5. Multiply it by 4 and subtract from the outer square area =
36 - 4 x 4 = 36 - 16 = 20 sq. in.
|
3). A parallelogram has vertices at
(2, 3), (-6, 0), and (-2, 5).
Where is its 4th vertex located? |
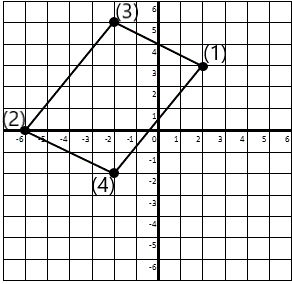The points are 1, 2 and 3 in the order listed.
Use this grid:
1. Plot the 3 points on the grid.
2. Determine the x and y offset of point 1 from point 3
(this is going from 3 to 1) = (+4,-2)
3. Apply this offset to point 2 = (-6+4,0-2) = (-2,-2).
|
