
Cartesian Coordinates - Where 2 lines cross
The equation of a line is
y = mx + b
Where m is the slope of the line
and b is the y-intercept
In the tutorial for finding an equation for a line we learned how to construct the equation in the form of y = m x + b given 2 points on the line.
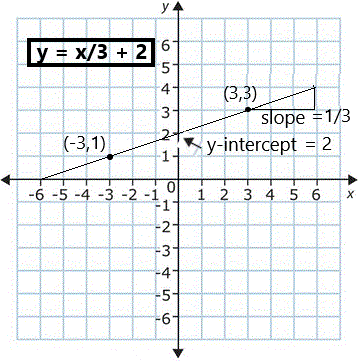
The equation we created from the 2 points (-3,1) and (3,3) is:
y = x/3 + 2 which looks like this =====>
We constructed it using the slope (m) of 1/3, meaning for every 3 x spaces the equation goes up 1 in y, and a y-intercept (b) of 2, which is where the equation crosses the vertical y-axis.
|
|
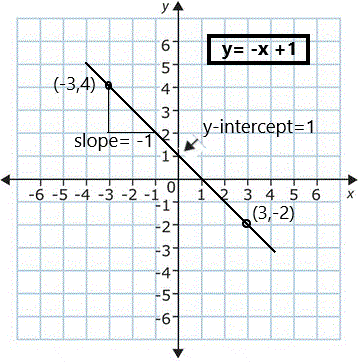
Now, what if we have a second equation, like the one that goes through points (-3,4) and (3,-2)? It looks like this ===>
You can see that for every one space in x you go down a space in y so the slope, m, is
If you put this slope into the equation, you get:
y = - x + b
So, b = y + x
and, using the first point's coordinates, (-3,4):
b = (+ 4) + (- 3) = 4 - 3 = +1
and the equation for it is:
y = - x + 1
|
|
Notice that equations with positive slope go "uphill" and those with negative slope go "downhill".
|
If we plot these 2 equations together it is easy to see that they cross, but where? Just from looking at their graphs, it looks like they cross somewhere near (-1,+2), but that is only approximate.
|
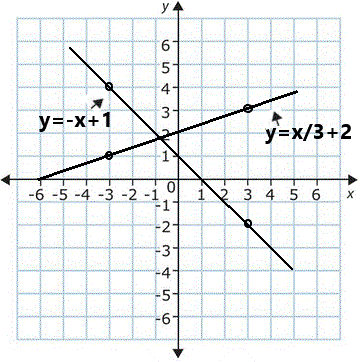
|
There must be a way to find out exactly where these 2 lines cross: where both equations have the same solution. Well, there is.
Here is how you find that point:
-
Set the 2 equations equal to each other
Since the 2 equations have the same solution (x,y) at the crossing point, if you set the y of one equation equal to the y value of the other equation, you should be able to find the x coordinate where they cross, like this:
- x + 1 = x/3 + 2
- Combine terms and solve for x
Combining terms and constants give us:
(4/3) x = -1
x = -3/4 <=== the x coordinate of the crossing point. Close to where we eyeballed it!
- Use this x to find the y crossing point
Now, using this x, put it into either one of the equations and you have your y-value.
Let's use the second equation:
y = - x + 1: <=== the second equation
y = - ( -3/4) + 1
y = +3/4 + 1 = 13⁄4
So, the crossing point is (-3⁄4 , 13⁄4)
We can check this by plugging this x value back into the first equation and seeing if we get the same y value, the crossing point:
- y = x/3 + 2 <=== the first equation
- y = (-3⁄4) / 3 + 2
- y = (-
3⁄4) (1⁄3) + 2 (the 3s cancel!)
- y = -1⁄4 + 2 = 13⁄4 <=== the correct y value!
|
|

