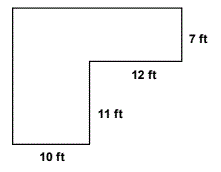
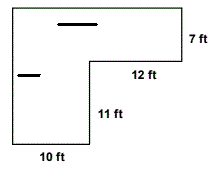
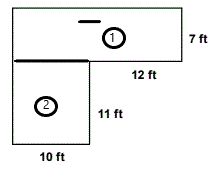
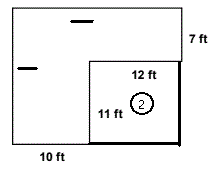
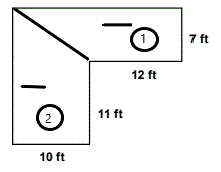
Areas of Composite Shapes

If you have a shape made of multiple geometric areas there are usually several ways to approach deterimining its area.

Consider this shape made up of rectangles:
*(2008 Olympiad, 5th grade measurement #1)*	First, label the unlabeled sides:

There are several ways to determine its area.

1). Cut it horizontally:

The two rectangles are
① _____ x _____ = ____ sq. ft.
+ ② _____ x _____ = ____ sq. ft.
Total area = _____ sq. ft.

2.) Cut it vertically:

The two rectangles are
① ____ x ____ = ____ sq. ft.
+ ② ____ x ____ = ____ sq. ft.
Total area = _____ sq. ft.

3). Area subtraction:

Complete the outer rectangle, ①, determine it's area and then subtract the missing rectangle, ②.
① = ___ x ___ = _____ sq. ft.
- ② = ___ x ___ = _____ sq. ft.
Total area = _____ sq. ft.

4). Cut into 2 trapezoids:
Area of a trapezoid =(b1 + b2) h / 2

① = ____________ = ____ sq. ft.
2
+ ② = ____________ = ____ sq. ft.
2
Total area = _____ sq. ft

Another common composite areas problem is like this

(2011 Olympiad, 6th grade geometry #2):
Find the area of the shaded area in this figure. The diameter of all the circles is 10 cm.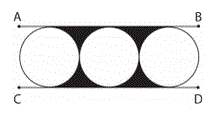

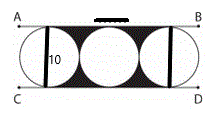1. The line segments AB and CD touch the circles at their half-way points.
2. Draw a rectangle whose corners are the points where the lines touch the outer circles on both the AB line and the CD line.
3. Compute the area of this rectangle and then subtract the areas of the included circles. There are 2 circles included in this rectangle. (one whole one and 2 halves)
4. Since the diameter of each circle is 10 cm., the width of the rectangle = ____ cm.
Rectangle area = ______ sq. cm.
5. Subtract the areas of the included circles to get the shaded area =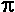
_______ - 2

R² =
_______ - 2 x 3.14 x _____ = _____ sq. cm.