Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2006 Grade 6 Geometry
Problem
1) A teacher places a plastic right triangle on the overhead projector to enlarge it so that the whole class can see it. It has a base of 5 cm and a height of 15 cm. If the image on the screen has a base of 20 cm, what is the area of the image triangle?
2) A cube sculpture is created from cubes stacked on top of each other and next to each other. Cubes that are stacked meet along their square faces. The top view, front view, and side view of a cube sculpture are given below, where only the squares directly facing you from each view point are shown. What is the least number of cubes you would need to add to the sculpture to make it a solid rectangular prism of cubes?
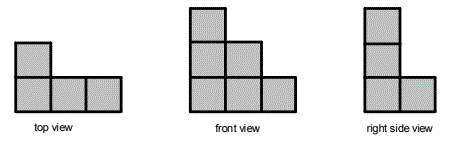
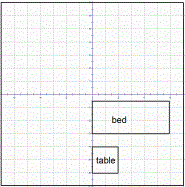3) Jill decides to rearrange her room. She will rotate the bed and table clockwise 90 degrees around the center of her room. The center of the room is given by the origin. The original coordinates of the table were
(0, -4), (2, -4), (2, -6), (0, -6).
What will be the new coordinates of the table?

Problem
4) An 8-inch square of thin paper is folded in half vertically and then horizontally to create a new square. These 2 folds are repeated 5 times each, including the first 2 folds, to create a tiny square. What is the perimeter of the new square? (An 8-inch square is a square that is 8 inches on each side.)
5) Andy wants to make circular flower beds that will be outlined with 4 meter lengths of plastic edging. What is the radius of the biggest circular flower bed he can make with one length of plastic edging? Give your answer to the nearest tenth of a meter.