 3) Jill decides to rearrange her room. She
will rotate the bed and table clockwise 90 degrees
around the center of her room. The center
of the room is given by the origin. The
original coordinates of the table were
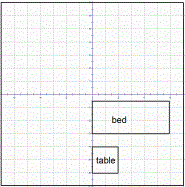
3) Jill decides to rearrange her room. She
will rotate the bed and table clockwise 90 degrees
around the center of her room. The center
of the room is given by the origin. The
original coordinates of the table were
(0, -4), (2, -4), (2, -6), (0, -6).
What will be the new coordinates of the table?
|
"Clockwise" means this way: ↷
This problem is asking for the coordinates of the table, not the bed.
- To rotate coordinates 90o clockwise means to negate the x coordinate and exchange the x and the y, like this:
(x,y) = (y,-x)
- Perform the rotations:
(0,-4) = (___,___)
(2,-4) = (___,___)
(2,-6) = (___,___)
(0,-6) = (___,___)
|
|
4) An 8-inch square of thin paper is folded in half vertically and then horizontally to create a
new square. These 2 folds are repeated 5 times each, including the first 2 folds, to create
a tiny square. What is the perimeter of the new square? (An 8-inch square is a square
that is 8 inches on each side.) |
1. Each fold halves the area of the square and there are 5 of these folds, so the final area is ____ of the original paper's area.
2. Compute the side length of the folded paper = ___ inches.
3. Compute the perimeter of the small resulting square = ____
|