| Problem |
Solution |
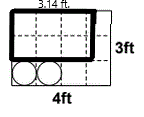 3) Julius is making a duffel bag out of a piece of canvas that measures 3 feet by 4 feet. It will be cylindrical with dimensions 2 feet long and diameter 1 foot. Disregard the seams. The two end pieces are sketched out. Sketch in the third
piece. How much canvas will be left over after he cuts out the pieces? Express your answer to the nearest tenth of a square foot. Use
3) Julius is making a duffel bag out of a piece of canvas that measures 3 feet by 4 feet. It will be cylindrical with dimensions 2 feet long and diameter 1 foot. Disregard the seams. The two end pieces are sketched out. Sketch in the third
piece. How much canvas will be left over after he cuts out the pieces? Express your answer to the nearest tenth of a square foot. Use 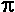 = 3.14 = 3.14 |
The circumference of one of the ends is the width of the rectangle you need to make the duffel bag.
1. Compute the circumference of one of the end circles.
C = 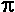 D = 3.14 x 1 = 3.14 ft. D = 3.14 x 1 = 3.14 ft.
2. This is the width of a rectangle that makes the duffel bag.
See the figure for how this fits.
3. Compute the area of the rectangular piece of canvas =
3.14 x 2 = 6.28 sq. ft.
4. Compute the area of one of the end circular pieces =
A = 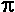 R2 = 3.14 x (1/2)2 = 3.14 x (1/4) = .785 sq. ft. R2 = 3.14 x (1/2)2 = 3.14 x (1/4) = .785 sq. ft.
5. Take the area of the whole piece of canvas, subtract the rectangular piece and 2 of the end pieces to get the area of canvas left over =
(3 x 4) - 2 x (.785) - 6.28 = 4.15 sq. ft.
Area left over (rounded) = 4.1 or 4.2 sq. ft.
|
 4) In the floor plan for a museum 8 revolving security cameras are shown as dots. They cover the whole floor plan. The owner wants to know: Can fewer cameras be used and where would they need to be mounted? Indicate number and location on the diagram on the answer sheet.
4) In the floor plan for a museum 8 revolving security cameras are shown as dots. They cover the whole floor plan. The owner wants to know: Can fewer cameras be used and where would they need to be mounted? Indicate number and location on the diagram on the answer sheet.
|
The lines are the walls of the museum. (Strange museum!) Put dots on the diagram on the corners such that cameras placed there can "see" into all the corners. Make sure all corners can be seen by at least one camera and use as few dots as possible. Assume there is no limit on the camera's range.

Any answer that uses 3 cameras that can "see" all corners is valid.
|
5) Leo makes an octahedron by gluing together two pyramids along their bases. Its surface area is 16
square inches. Each triangle has a height of 2 inches. What is the surface area of one of the pyramids?
|
1. An octahedron has 8 triangular sides.
2. Divide the total surface area by 8 to get
the area of one triangle = 16/8 = 2 sq. in.
3. A pyramid has a square base and 4 triangular sides.
4. Since you have the area of one of the triangular sides, all you need now is the area of the pyramid's square base. To get that you need to know the length of one of the trianglular bases. You can get that using the triange area and height information.
B = 2A/H = (2 x 2)/2 = 2 in.
Square base area = 2 x 2 = 4 sq. in.
5. Add this to 4 of the triangular areas to get the total pyramid area =
4 + (4 x 2) = 4 + 8 = 12 sq. in.
|