| Problem |
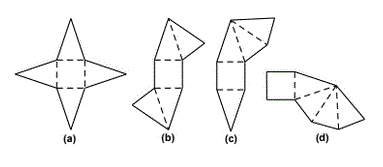
3) Each figure below is made up of 1 square and 4 congruent isosceles triangles.
The interior dotted lines are fold lines. Which of these
figures can be folded to make pyramids with a square base?
 |
4) The coordinates of the vertices of a quadrilateral in
clockwise order are: (0, 3), (4,8), (8,3), and (4, 5).
What is its area?
|
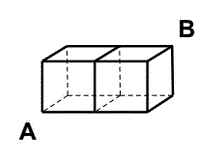5) The length of the shortest trip from A to B along the
edges of the cube shown is 4 edges. How many different
4-edge trips are there from A to B?
|
|
1) The 
units. It has center B. The shaded region has half the area of the unshaded region. What is the perimeter of the shaded region? Express your answer to the nearest tenth of a unit. Use 
2) Line segments AB and CD are parallel. The three circles
in between them just touch each line segment at one point
and the circles touch each other at one point. Each circle
has a diameter of 10 units. Find the area of the shaded
areas in between the circles to the nearest square unit.
Use