Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2011 Grade 6 Geometry
Problem
Solution
1) The circumference of the circle shown is 6 units. It has center B. The shaded region has half the area of the unshaded region. What is the perimeter of the shaded region? Express your answer to the nearest tenth of a unit.
Use = 3.14 if needed.
 1. The formula for the circumference is
    C = D so,
    6 = D
    so D must be 6
2. Segments AB and BC are radii,
    so their length is (6/2) = 3
3. Since the shaded region is half the unshaded region, then it is 1/3 of the circle and the portion of the circumference from A to C is 1/3 of the circumference.
4. Add 2 of the radii and this AC circumference segment length to get perimeter of the shaded region =
    3 + 3 + 2 = 6 + 2 x 3.14 =
    12.28 units, rounded = 12.3 units
2) Line segments AB and CD are parallel. The three circles in between them just touch each line segment at one point and the circles touch each other at one point. Each circle has a diameter of 10 units. Find the area of the shaded areas in between the circles to the nearest square unit.
Use = 3.14 if needed.
1. The line segments AB and CD touch the circles at their half-way points.
2. You can make a rectangle whose corners are the points where the lines touch the outer circles on both the AB line and the CD line. Draw in that rectangle.
3. The idea here is to compute the area of this rectangle and then subtract the areas of the included circles. There are 2 circles included in this rectangle.
4. Since the diameter of each circle is 10 units, compute distance on the AB line from the first 'touch' point to the last one = 20
5. Using this and the diameter of the circles, compute the area of the rectangle = 20 X 10 = 200.
6. Subtract the areas of the included circles to get the area of the shaded portion =
    200 - 2(R2) = 200 - 2(3.14 X 25) =
   200 - 157 = 43 square units.

Problem
Solution
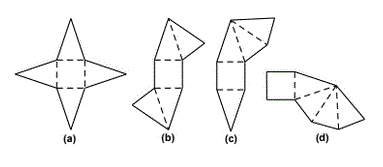
3) Each figure below is made up of 1 square and 4 congruent isosceles triangles. The interior dotted lines are fold lines. Which of these figures can be folded to make pyramids with a square base? Here is a pyramid: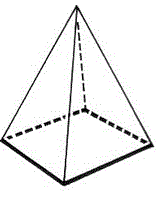
Study it and imagine each of the 4 figures folded into this shape.

Hint: more than one of the shapes can be folded into a pyramid, but not all.
The only figure that doesn't fold into a pyramid is (c) because that upper right triangle, when folded, overlaps the triangle on the bottom.
So, the figures that can be folded into pyramids are
    a, b and d
4) The coordinates of the vertices of a quadrilateral in clockwise order are: (0, 3), (4,8), (8,3), and (4, 5). What is its area?
Plot the points on the grid and number them.
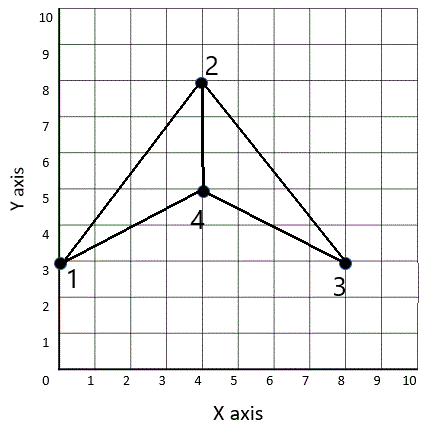Method 1: Cut into triangles and add:
1. Notice that the 2nd and 4th points have the same x coordinate = 4.
2. Cut the quadrilateral into two triangles along this vertical y-line (4,8) to (4,5)
    (1) = points 1,2 and 4:
        B = 3, H = 4, A = 6
    (2) = points 2,4 and 3: B = 3, H = 4, A = 6
3. Compute the areas of each triangle and add:
    A = 6 + 6 = 12 sq. units
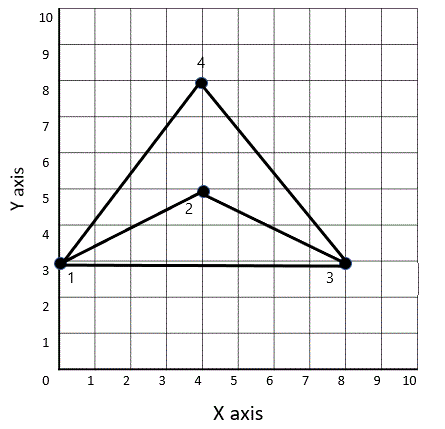Method 2: Area subtraction:
Make a large triangle and subtract the missing triangle:
1. Compute the area of the triangle made by
    points 1, 2 and 3 = B = 8, H = 5, A = 20
2. Compute the area of the triangle made by points 1, 4 and 3 =
    B = 8, H = 2, A = 8
3. Subtract the second from the first to get
    the quadrilateral area = A = 20 - 8 = 12 sq. units
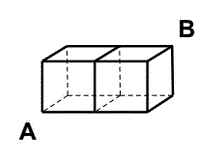5) The length of the shortest trip from A to B along the edges of the cube shown is 4 edges. How many different 4-edge trips are there from A to B? 1. The number of paths from point A are 3.
2. From that point (assuming you don't go backward
    or away from B) there are 2 paths forward.
3. From that point there are 2 paths to get to B.
4. From that point there is 1 path to get to B and you are there!
5. Multiply all these paths together to get the total number of possible paths =
    3 x 2 x 2 x 1 = 12 ways