| Problem |
Hint |
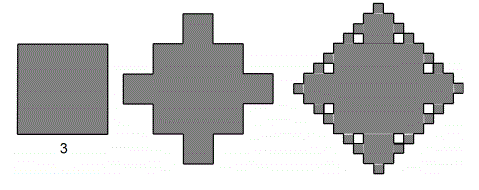
3) The first figure is a square with side length 3 units. The second figure is obtained from
the first by replacing each middle third of a side with three sides of a square. The third
figure is obtained from the second by replacing each middle third of a side with three sides
of a square. What is the area of the third figure? The third figure is not accurately drawn,
it is there to help you visualize.
Express your answer as a mixed number.
|
Tough problem! ... but let's get started:
1. The area of the first square = _____
2. The second figure adds 4 squares whose sides are 1/3 of the big square sides. The added sides are ____ units, The individual squares area is ____ units, and 4 of them add _____ sq. units.
3. The sides of the little squares in the 3rd figure are 1/3 of the sides in the second figure = _____ units. Their area is _____ sq. units
4. Count the number of edges in the second figure. There are ____ of them.
5. If you look close, each of the edges in the second figure has a little square on it in the 3rd figure. There is one for each edge, so this adds _____ sq. units to the total area.
6. Now, add the area of the first square ____, the added area of the small squares in the second figure _____, and the added area from the previous step = _____ sq. units.
|
4) At twelve noon the angle between the hour and minute hands on an analogue clock is
0 degrees. What is the angle between the hands on the clock at 12:30 pm? (30 minutes later)
|
This problem isn't as easy as it sounds, because as the minute hand moves from 0 to 30 minutes (half a revolution), the hour hand is moving also.
1. For an hour, the hour hand moves through this fraction of a revolution = _____ degrees.
2. For half an hour it moves half that much = _____ degrees.
3. The angle between the hour hand at the above angle and the minute hand is _____ degrees.
|
|
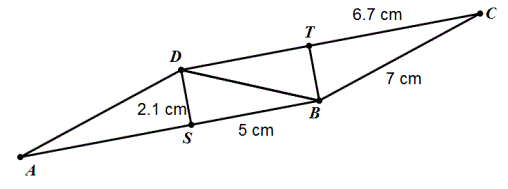
5) To find the area of parallelogram ABCD, Drew draws the perpendicular segments DS
and BT. He does some measuring. To the nearest tenth of a centimeter BC = 7 cm, CT =
6.7 cm, BS = 5 cm, and DS = 2.1 cm. If he has enough information to compute the area of
parallelogram ABCD, then compute the area to the nearest tenth of a square centimeter. If
he needs to make more measurements, list the segments he needs to measure.
|
The area of a parallelogram is base x height.
1. The base of the parallelogram is AB or DC.
2. The height is DS = ____ cm.
3. Use the TC length and the SB length to find the length of AB = ______
4. Multiply the two to get the area = ______.
|