| Problem |
Solution |
2) An isosceles trapezoid has a line of symmetry. Three
of the vertices of the isosceles trapezoid are
(1, 6 ),
(3, 2), and (7, 2) as shown.
The fourth vertex has whole
number coordinates. What are the coordinates of the
fourth vertex?
|
1. Draw the 2 sides that are given by the 3 points.
2. One of the bases of the trapezoid is the line from point 2 to point 3.
3. Draw a line from point 1 parallel to the base you drew.
4. Locate a point on that line that makes the trapezoid isosceles (sides other than the bases are equal).
5. Draw the 4th side. It should be symmetric with the other side.
6. The coordinates of point 4 are (9,6).
|
3) The first figure is a square with side length 3 units. The second figure is obtained from
the first by replacing each middle third of a side with three sides of a square. The third
figure is obtained from the second by replacing each middle third of a side with three sides
of a square. What is the area of the third figure? The third figure is not accurately drawn,
it is there to help you visualize.
Express your answer as a mixed number.
|
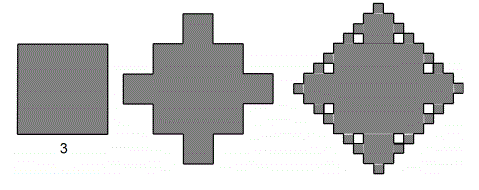
Tough problem! ... but let's get started:
1. The area of the first square = 9
2. The second figure adds 4 squares whose sides are 1/3 of the big square sides. The added sides are 1 unit, The individual squares area is 1 unit, and 4 of them add 4 sq. units.
3. The sides of the little squares in the 3rd figure are 1/3 of the sides in the second figure = 1/3 unit. Their area is 1/9 sq. unit each
4. Count the number of edges in the second figure. There are 20 of them.
5. If you look close, each of the edges in the second figure has a little square on it in the 3rd figure. There is one for each edge, so this adds 20 x 1/9 = 20/9 = 2 2/9 sq. units to the total area.
6. Now, add the area of the first square 9, the added area of the small squares in the second figure 4, and the added area from the previous step = 2 2/9 = 15 2/9 sq. units
|
|
Note: There is a solution that gets 23 tickets onto the sheet (see figure to the right), but it requires two different configurations and needs to be sketched out on a sheet of graph paper, which the students don't have, therefore I have eliminated consideration of that solution.
This problem isn't as easy as it sounds, because as the minute hand moves from 0 to 30 minutes (half a revolution), the hour hand is moving also. See the figure to the right.