Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2015 Grade 5 Geometry
Problem
Hint
1) Ahmed is trying to make a parallelogram on the given coordinate grid. A, B, C are three corners of the parallelogram. If he wants to complete the figure in quadrant III, where should the final point go?
1. Quadrant III is the lower left quadrant where X and Y are both negative.
2. To make a parallelogram, the offset of A to the new point D should be the same as the offset of point B to point C which is (___,___).
3. Apply this offset to A to get the 4th point = (___,___).

2) What is the angle between the hour and minute hands of an analog clock at 3:30 pm?


 1. Minute hand: is at 30 minutes which is _____ degrees from 0 degrees.
2. In one hour the hour hand moves ____ degrees from 0.
3. In 3.5 hours it moves _____degrees.
4. Subtract these two angles = _____

Problem
Hint

3) The rectangle shown is divided evenly into squares. Each square has an area of 25 square centimeters. What is the perimeter of the rectangle?
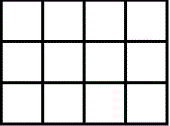
 1. If each of the squares has an area of 25 sq. cm, then one side of the square is _____ cm.
2. Compute the perimeter given this measurement = _____ cm.

4) Lenore is filling a box measuring 14 inches by 6 inches by 10 inches with cubes measuring 2 inches to a side. With the box standing at its tallest, she has filled one layer with the cubes. How many more cubes will she need to fill the box?		 1. The tallest side of the box is ____ inches.
2. If the box is standing at its tallest, then the base it is standing on is ____ by _____ inches.
3. Compute the area of one cube face = ____ sq. in.
4. Compute the area of the base = ____.
5. Divide this area by the area of one cube face = _____ cubes.
6. Compute the volume of one little cube = ____ cu. in.
7. Compute the volume of the box = _____.
8. Divide this volume by the volume of one cube to get the total number of cubes in the box = _____.
9. Subtract the number of cubes in that bottom row to get the number she will need to fill the box = _____.
5) A 16 in x 16 in square piece of paper is folded in half to form a triangle. That triangle is folded in half again three more times. If the original paper has a side length of 16 inches, what is the area of the last triangle after folding? 1. After the square piece of paper is folded it makes a triangle whose area is _____ sq. in.
2. With each fold after the first fold the area of the triangle is halved.
3. The number of halvings is 3.
4. The area of the last triangle is therefore _____ of the original triangles area = _____ sq. in.