| Problem |
Hint |
3). What is the area of the polygon shown in the
figure?
(Figure is not to scale)
|
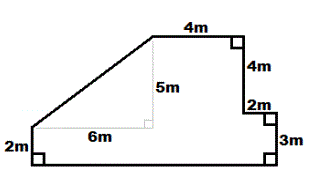
Method 1:Cit it up into a triangle and 3 rectangles.
OK, how to cut this up? Many ways, but vertical cuts look the easiest:
1. Draw a vertical cut along the 5 m side of the triangle.
2. Draw a second vertical cut making a little 2 x 3 rectangle in the lower right corner.
3. Compute the area of the triangle = _____ sq. m.
4. Compute the area of the 3 rectangles = _____ sq. m.
5. Add them for the total area of the figure = ____ sq. m.
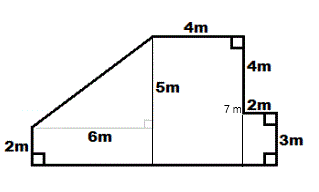
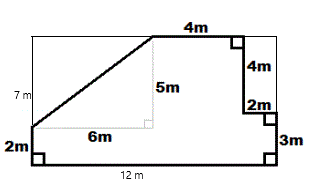Method 2: Use area subtraction:
Complete the outer rectangle, compute it's area and subtract the triangle and the rectangle = _____
|
4) What is the angle between the hour and minute hands of a standard clock face at 5:00 pm?
|
1. In one hour, the hour hand of a clock moves ___ degrees.
2. At 5 pm, the hour hand makes a _____ degree angle from 12 o'clock.
3. The minute hand is pointed at 0( straight up).
4. The angle between them is ____ degrees.
|
5) If the trapezoid is moved 6 spaces down and rotated 90o
counter clockwise around A. What is the coordinate of B?
|
- Counter clockwise is this way: ↶
- The coordinates of B are (___,___) and A is (___,___)
- When you move it down 6 spaces, their new coordinates are:
A = (___,___) and B = (___,___)
- Draw these coordinates on the graph.
- To
rotate one point 90 degrees counterclockwise around another:
- Determine the offset of point A from point B by subtracting B from it: A - B = (___,___) - (___,___) = (___,___)
- To rotate a point counterclockwise around another you exchange coordinates and negate the y coordinate:
(x,y) => (-y,x), so B: (___,___) becomes (___,___)
- Add the coordinates of A back:
(___,___) + (___,___) = (___,___)
|
|
1) What is the measure of angle X?