Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2016 Grade 5 Geometry
Problem
Solution
1) What is the measure of angle X?
(Figure is not to exact scale)		 1. Note the right triangle in this figure.
2. The unlabeled angle of the right triangle is complementary with the 41o angle and is 49 degrees.
3. Angle X is vertical with this angle and is also 49 degrees.
2) The largest angle of an isosceles triangle is 114 degrees. What is the measure of each of the other two angles?
 1. The angles of a triangle all add up to 180 degrees.
2. Because the triangle is isosceles, the other two angles are the same measure, which is (180 - 114)/2 = 66/2 = both 33 degrees.

Problem
Solution
3). What is the area of the polygon shown in the figure?
(Figure is not to scale)
 Method 1: Cut it up into a triangle and 3 rectangles.
OK, how to cut this up? Many ways, but vertical cuts look the easiest:
1. Draw a vertical cut along the 5 m side of the triangle.
2. Draw a second vertical cut making a little 2 X 3 rectangle in the lower right corner.
3. Compute the area of the triangle =
    (6 x 5)/2 = 15 sq. m.
4. Compute the area of the 3 rectangles
    rectangle #1: 2 x 6 = 12 sq. m. (lower left)
    rectangle #2: 7 x 4 = 28 sq. m. (big middle one)
    rectangle #3: 3 x 2 = 6 sq. m. (tiny one in the lower right corner)
5. Add them for the total area of the figure =
  15 + 12 + 28 + 6 = 61 sq. m.

Method 2: Use area subtraction:
Complete the outer rectangle, compute it's area and subtract the triangle and the rectangle =
    outer rectangle = 7 x 12 = 84 sq. m.
    triangle = (6 x 5) /2 = = 15 sq. m.
    little rectangle = 4 x 2 = 8 sq. m.
    Total = 84 - 15 - 8 = 61 sq. m.

Problem
Solution
4) What is the angle between the hour and minute hands of a standard clock face at 5:00 pm? 1. In one hour, the hour hand of a clock moves 30 degrees.
2. At 5 pm, the hour hand makes a 150 degree angle from 12 o'clock.
3. The minute hand is pointed at 0( straight up).
4. The angle between them is 150 degrees.
5) If the trapezoid is moved 6 spaces down and rotated 90o counter clockwise around B, what is the coordinate of B?
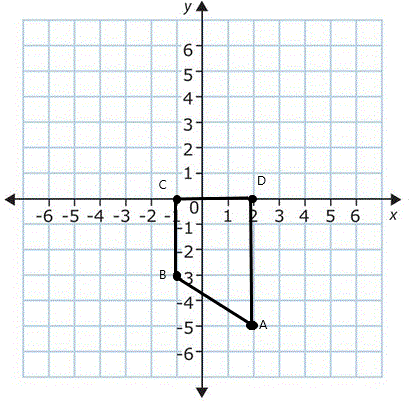
  1. Counter clockwise is this way: ↶
  2. The coordinates of B are (4,4) and A is (2,1)
  3. When you move it down 6 spaces, their new coordinates are:
    A = (4,-2) and B = (2,-5)
  4. Draw these coordinates on the graph.
  5. To rotate one point 90 degrees counterclockwise around another:
    1. Determine the offset of point A from point B by subtracting B from it: A - B = (4,-2) - (2,-5) = (2,3)
    2. To rotate a point counterclockwise around another you exchange coordinates and negate the y coordinate:
      (x,y) => (-y,x), so B: (2,3) becomes (-3,2)
    3. Add the coordinates of A back:
      (-3,2) + (2,-5) = (-1,-3)
The figure to the left is the trapezoid aftr all the moves.