| Problem |
Solution |
1) A square can be split to make four smaller
squares of equal sizes to completely fill the
original square as shown. How would you split up
the original square into six smaller squares that
completely fill the original square without any
overlaps of the smaller squares?
(The squares do
not all need to be the same size.)
|
1. Cut the square into 9 equal sized smaller ones.
2. You should be able to solve this once you look at this diagram by combining these smaller squares.
The answer should look like this:
Any combination of 4 smaller squares to make a larger square are OK.
|
2) If the total surface area of a cube is 150 sq. cm., what is its volume?
|
1. The surface area consists of 6 of the faces.
2. Set this equal to 150 and solve for the length of a side: =
6A = 150
A = 25
S (the length of a side = 5 cm.
3. Compute the volume as the side length cubed =
53 = 125 cu. cm.
|
3) In rectangle ABCD, X is the midpoint of CD and
Y is the midpoint of AD. What percentage of the
figure does the shaded area represent?
|
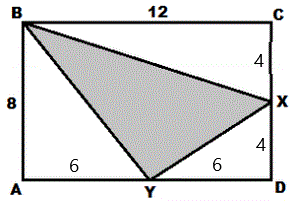
1. Put the length of the sides XC, XD, AY and YD on the figure.
2. Compute the sum of the areas of the 3 non-shaded triangles:
A1 = (6 x 8)/2 = 24
A2 = (12 x 4)/2 = 24
A3 = (4 x 6)/2 = 12
A1 + A2 + A3 = 60
3. Subtract this from the area of the rectangle =
(8 x 12) - 60 = 96 - 60 = 36
3. Divide this by the area of the rectangle =
36/(8 x 12) = 6/16 = 3/8
4. Convert 3/8 to percent =
3 / 8 = .375 x 100 = 37.5%
|
