Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2017 Grade 5 Geometry
Problem
Hint
1) What is the measure of angle X?
(Figure is not to exact scale) 		Call the missing angles a (the one that is supplementary with the 93o angle), b (the one next to x) and c (the top one)

Method 1: Use angles a and b
1. Since angle a is supplementary with the 93o angle its value is ______ degrees.
2. Angle b is 180 - 64 - _____ = ______ degrees.
3. Angle b, angle x and the right angle add to 180o,
so the value of x = _______ degrees

Method 2: Use angle c
1. Since angle x and angle b sum to 90 degrees, the value of angle c is _______ degrees.
2. Since angle x, angle c and the 93 degree angle sum to 180 degrees, the value of angle x = _________ degrees

2) A square has vertices at (2,-1) and (-5,2). Only one of its vertices is in Quadrant III. Give the coordinates of the vertex that is in Quadrant III.
 Use the grid to the left to plot the two points.
1. Since only one vertex is in Quadrant III, the two given points cannot be one side of the square or (a) both of the other vertices would be in Quadrant III or (b) neither would be in Quadrant III, so they must be on opposite corners of the square.
2. The new vertex is equidistant from both of these points.
3. Find a point in Quadrant III for whom the sum of its X and Y offsets from point 1 are the same as the sum of its X and Y offsets from point 2 by plotting points on the grid and computing their (X + Y) offsets from both points until you find a point where they add to the same value.
The Quadrant III point is (___,___).

Problem
Hint

3) Find the area of the figure:
    Method 1 (horizontal cut) diagram:

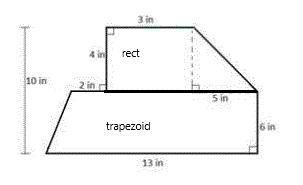
    Method 2 (vertical cuts) diagram:
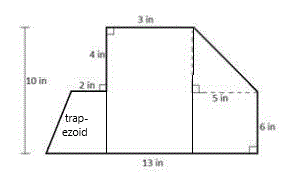
 Method 1: Draw a line horizontally that is along the 5 inch side of the inscribed triangle.
That results in 3 figures: 1 rectangle, 1 triangle and 1 trapezoid on the bottom. So, here we go:
1. Compute the area of the triangle = ____ sq. in.
2. Compute the area of the rectangle on the top = ____ sq. in.
3. Write in the length of the line you drew to cut the figure = ____ in.
4. Compute the area of the trapezoid using the area formula for a trapezoid:
  A = (b1 + b2) h / 2, where:
  b1 = length of one base,
  b2 = length of the other base, and
  h = height of the trapezoid. A = _____ sq. in.
5. Add these to get the total area of the figure = _____ sq. in.

Method 2: Draw vertical lines that cut the figure into 2 rectangles, a trapezoid and a triangle:
1. Compute the area of the triangle = ____ sq. in.
2. Compute the area of the big middle rectangle = ____ sq. in.
3. Compute the area of the small rectangle = ____ sq. in.
4. Write in the length of the base of the trapezoid = ____ in.
5. Compute the area of the trapezoid using the area formula for a trapezoid:
  A = (b1 + b2) h / 2, where:
  b1 = length of top base,
  b2 = length of the other base, and
  h = height of the trapezoid. A = _____ sq. in.
6. Add these to get the total area of the figure = _____ sq. in.

4) The point (5,-3) is reflected across the x-axis, moved left 2 units and then reflected across the y- axis. What are the coordinates of the new point? 		Use the grid on problem 2 to plot these points.
1. To "reflect across the x-axis" means to change the sign of its Y coordinate. That point (reflected) is (___,___)
2. Now move it left 2 units (subtract 2 from the X coordinate) = (___,___)
3. To "reflect across the y-axis" means to change the sign of the new point's X coordinate. That new point
(now reflected twice) is (___,___)

Problem
Hint

5) An equilateral triangle has an area of 64 sq. in.

The midpoints of the sides are connected and the middle triangle shaded in:
 Each of the remaining unshaded triangles is now changed in the same way: This is done one more time, creating this triangle:


What is the area of the unshaded region in this third triangle?
1. The idea is to subtract all the shaded triangles from the figure, leaving only unshaded triangles. There are 3 sizes of these triangles: large, mid-size and small:
2. Large: The large shaded triangle in the first figure is ____ of the total figure. Since the total area of the big triangle is 64 sq. in., the size of this large shaded triangle is ____ sq. in.
3. Mid-size: The mid-sized shaded triangles in the second figure which are ____ the area of the large shaded triangle in the first figure. The area of these triangles is ____ sq. in.
4. Small: The small shaded triangles in the third figure are ____ the area of the mid-sized shaded triangles. Their area is ____ sq. in.
5. Count up the number of each size shaded triangle, add their areas and subtract from the total area,
= _____ sq. in.