Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2017 Grade 5 Geometry
Problem
Solution
1) What is the measure of angle x?
(Figure is not to exact scale)
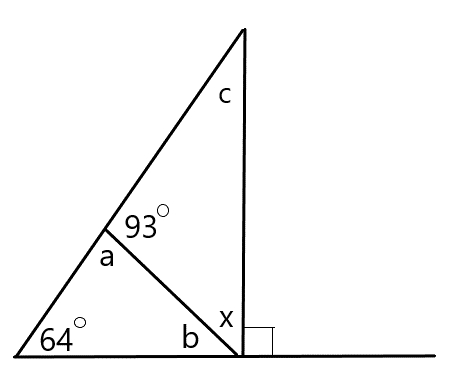
Call the missing angles a (the one that is supplementary with the 93o angle), b (the one next to x) and c (the top one)

Method 1: Use angles a and b
1. Since angle a is supplementary with the 93o angle its value is
180 - 93 = 87 degrees.
2. Angle b is 180 - 64 - 87 = 29 degrees.
3. Angle b, angle x and the right angle add to 180o,
so the value of x = 180 - 90 - 29 = 61 degrees

Method 2: Use angle c
1. Since angle x and angle b sum to 90 degrees, the value of angle c is 180 - 90 - 64 = 26 degrees.
2. Since angle x, angle c and the 93 degree angle sum to 180 degrees, the value of angle x = 180 - 93 - 26 = 61 degrees

2) A square has vertices at (2,-1) and (-5,2). Only one of its vertices is in Quadrant III. Give the coordinates of the vertex that is in Quadrant III.
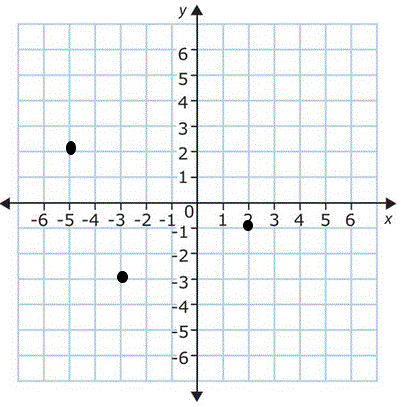
 Use the grid to the left to plot the two points.
1. Since only one vertex is in Quadrant III, the two given points cannot be one side of the square or (a) both of the other vertices would be in Quadrant III or (b) neither would be in Quadrant III, so they must be on opposite corners of the square.
2. The new vertex is equidistant from both of these points.
3. Find a point in Quadrant III for whom the sum of its X and Y offsets from point 1 are the same as the sum of its X and Y offsets from point 2 by plotting points on the grid and computing their (X + Y) offsets from both points until you find a point where they add to the same value.
The offsets of point(-3,-3) is (5,2) from the first point and
(2,5) from the second point, which makes that point equidistant from both given points.
The Quadrant III point is (-3,-3)

Problem
Solution

3) Find the area of the figure.
    Method 1 (horizontal cut) diagram:

    Method 2 (vertical cuts) diagram:
 Method 1: Draw a horizontal line that is along the 5 inch side of the inscribed triangle. That results in 3 figures: 1 rectangle, 1 triangle and 1 trapezoid on the bottom. So, here we go:
1. Compute the area of the triangle =
    (5 x 4) / 2 = 10 sq. in.
2. Compute the area of the rectangle on the top =
    4 x 3 = 12 sq. in.
3. Write in the length of the line you drew to cut the figure = 10 in.
4. Compute the area of the trapezoid using the area formula for a trapezoid:
    A = (b1 + b2)h / 2, where:
    b1 = length of one base,
    b2 = length of the other base, and
    h = height of the trapezoid.
    A = ((10 + 13) X 6) / 2 = 138 / 2 = 69 sq. in.
5. Add these to get the total area of the figure =
    10 + 12 + 69 = 91 sq. in.

Method 2: Draw vertical lines that cut the figure into 2 rectangles, a trapezoid and a triangle:
1. Compute the area of the triangle = (5 x 4) / 2 = 10 sq. in.
2. Compute the area of the big middle rectangle = 3 x 10 = 30 sq. in.
3. Compute the area of the small rectangle = 5 x 6 = 30 sq. in.
4. Write in the length of the base of the trapezoid = 13 - 8 = 5 in.
5. Compute the area of the trapezoid using the area formula for a trapezoid:
  A = (b1 + b2) h / 2, where:
  b1 = length of top base,
  b2 = length of the other base, and
  h = height of the trapezoid.
    A = (2 + 5) x 6/2 = 21 sq. in.
6. Add these to get the total area of the figure =
    10 + 30 + 30 + 21 = 91 sq. in.

Problem
Solution
4) The point (5,-3) is reflected across the x-axis, moved left 2 units and then reflected across the y- axis. What are the coordinates of the new point? The grid to the left shows these points.
1. To "reflect across the x-axis" means to change the sign of its Y coordinate. That point (reflected) is (5,3)
2. Now move it left 2 units (subtract 2 from the X coordinate) = (3,3)
3. To "reflect across the y-axis" means to change the sign of the new point's X coordinate. That new point
(now reflected twice) is (-3,3)
5) An equilateral triangle has an area of 64 sq. in.
The midpoints of the sides are connected and the middle triangle shaded in:
 Each of the remaining unshaded triangles is now changed in the same way: This is done
one more time,
creating this
triangle:
What is the area of the unshaded region in this third triangle?
1. The idea is to subtract all the shaded triangles from the figure, leaving only unshaded triangles. There are 3 sizes of these triangles: large, mid-size and small:
2. Large: The large shaded triangle in the first figure is 1/4 of the total figure. Since the total area of the big triangle is 64 sq. in., the size of this large shaded triangle is 16 sq. in.
3. Mid-size: The mid-sized shaded triangles in the second figure which are 1/4 the area of the large shaded triangle in the first figure. The area of these triangles is 4 sq. in.
4. Small: The small shaded triangles in the third figure are 1/4 the area of the mid-sized shaded triangles. Their area is 1 sq. in.
5. Count up the number of each size shaded triangle, add their areas and subtract from the total area,
1 large + 3 mid-size + 9 small =
16 + 3 X 4 + 9 X 1 = 16 + 12 + 9 = 37 sq. in. of shaded region, so the unshaded area is 64 - 37 = 27 sq. in.