Hands-on math!

Washington State Math Olympiad
Hints and Solutions
2008 Grade 6 Geometry
Problem
Hint
1) Toleen's math teacher makes a model of a solid rectangular prism out of white one centimeter cubes to explore surface area and volume. She paints the entire outside surface red. If the dimensions of the prism are 3 cm by 4 cm by 6 cm, how many of the cubes have exactly two sides painted red? 1. The cubes which have 2 sides painted are the edges that are not on the corners.
2. There are ___ 3 cm edges, ____ 4 cm edges and ___ 6 cm edges.
3. Subtract 2 for each edge (for the corners) and then multiply by the above numbers to get the total number of edge cubes that are not corners = _____
2) In right triangle AMC (see diagram) triangles ANP and PLC are similar. MNPL is a square. Segment MC has length 6 units and segment LC has length 4 units. What is the area of triangle ANP?
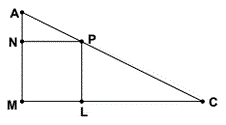
Similar means the triangles are the same shape but not the same size.
1. Write the lengths of MC and LC on the diagram.
2. Compute the length of a side of the square (ML and NP) = ___ units and write those lengths on the diagram.
3. Since the triangles are similar,
    the scale factor of the triangles is NP/LC = _____
4. Apply this scale factor to NP to get the length of AN = ______
5. Compute the area of ANP using the
    lengths of NP and AN = _____ sq. units
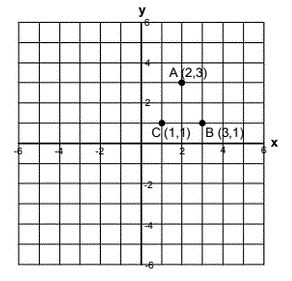
3) The points of an isosceles triangle are A=(2,3), B=(3,1), and C=(1,1). If you rotate the triangle 180 degrees about the origin and then reflect the triangle across the x-axis, what are the new coordinates for A, B, and C? 1. If you rotate the triangle 180 degrees around the origin that puts it in quadrant III upside-down. Perform that and draw in the new points in that quadrant.
2. If you rotate the triangle across the x-axis that puts it into quadrant II, right-side up again. Draw in those points.
3. The new coordinates are
A: = (___,___), B: (___,___), C: (___,___).

Problem
Hint
4) A dart board has a bull's-eye surrounded by 5 rings. The bull's-eye and the second and fourth rings are shaded (see diagram). If the bull's-eye has a radius of 2 cm, and each ring has a width of 2 cm, what is the area of all the shaded regions combined? Express your answer in terms of .
 1. The radius of the outer shaded circle is ____ cm.
2. The radius of the inner edge of that circle is ____ cm.
3. Compute the area of this ring using these two radii (keep the answer in terms of ). = _____ - _____ = _____
4. The radius of the inner shaded circle is ____ cm.
5. The radius of the inner edge of that circle is ____ cm.
6. Compute the area of this ring using these two radii
    (keep the answer in terms of ). = _____ - _____ = _____
7. Now, add the area of the bulls-eye to each of these areas
    to get the total = _____
5) When Andreyev wants to finish building the frame of the front of his club house he notices that things aren't quite right. The right post has a bit of a lean inwards and that messes with the top beam. What is the angle between the left post and the top beam? See diagram. There are 2 ways to approach this problem:
Method 1:
1. Compute the size of the angle adjacent to the 92.12o angle that is supplementary with it = _____
2. Since the angles of a rectangle all add up to 360o, the angle ? = _____.
Method 2:
You don't have to compute anything! Because 2 of the angles of the club house are 90o, that makes a special relationship between the ? angle and the unlabeled angle that is the same relationship the unlabeled angle has with the 92.12o angle.
Therefore, angle ? = _______.