| Problem |
Hint |
1) What is the area of the shaded portion of the circle of radius 5 units? Point P is the center of the
circle. You may give an exact answer or an approximation to the nearest tenth using the
approximation 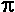 = 3.14. = 3.14.
 |
1. Compute the total angle at point P of the white sector = ____
2. Compute the fraction of the total square area the shaded area is ______
3. Compute the area of the total circle =_______.
4. Multiply this by the fraction of it that is shaded = _____
|
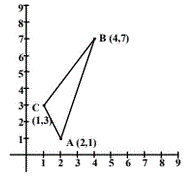 2) The formula for the area of a triangle is often gotten by looking at a related parallelogram. For
triangle ABC shown on the coordinate grid what are the coordinates of the vertices of a
parallelogram in the first quadrant that has twice the area of the triangle and contains the triangle?
2) The formula for the area of a triangle is often gotten by looking at a related parallelogram. For
triangle ABC shown on the coordinate grid what are the coordinates of the vertices of a
parallelogram in the first quadrant that has twice the area of the triangle and contains the triangle?
|
1. If you complete the parallelogram using the 3 given points you will double the triangle area.
2. Compute the offset of point A from point C
(this is C - A) = (___,___).
3. Apply this offset to point B to compute point D
that completes the parallelogram = (___,___)
|
|
3) The surface area of a rectangular prism box is 288 square inches. Another rectangular prism box
has double each dimension so twice the length, twice the width and twice the height or the first box.
What is its surface are
a?
|
Doubling each dimension increases the surface area
by a factor of (2 x 2) = 4.
New area = _____
|