| Subject | Problem | Solution | Other Problems
of this type |
Prob
& Stat | Problem type: Find missing number of a list given the average
Example: 2016 5th grade Prob Stat #1:
Julian has scored 93 and 96 on his first two tests. With one test remaining, what is the least score
Julian needs to average 90 or better on his three tests?
| This is actually an algebra problem.
The equation for the average (mean) is:
(93 + 96 + N) / 3 = 90.
Solve this equation for N = ____.
|
|
Measure-
ment | Problem type: Areas of composite shapes
Example: 2008 5th grade measurement #1:
How much carpeting is needed to cover the floor of an L shaped room with the dimensions shown in the figure?
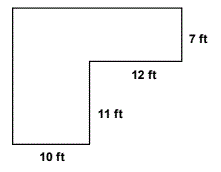 |
This is typical of a whole class of measurement problems that require the student to cut up a complex figure into rectangles, triangles and circle segments.
1. Write in the dimensions of the missing sides on the diagram.
2. Cut the figure into two rectangles.
3. Find the area of each rectangle and add them together.
|
|
| Algebra | Problem type: Algebraic sequences
Example: 2009 5th grade algebra #3:
Pictured is a sequence of growing chairs. The first chair is made of 6 squares. How many more squares are in the 8th chair in the sequence than in the first?
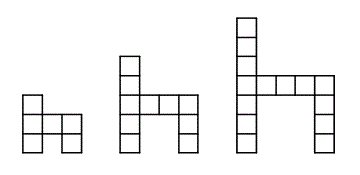 |
This is a sequence problem
1. Write out the sequence of numbers of squares in each chair:
6 ... 10 ... 14 ...
2. This is an arithmetic sequence where ___ is added to each element to get the next one.
3. The 8th chair has ___ squares.
4. Subtract the original number of squares in the first chair to get the answer: _____
|
|
| Algebra | Problem type: Guess-and-check
Example: 2016 5th grade algebra #4:
A farm keeps chickens (with 2 legs) and pigs (with 4 legs) in a pen. There are a total of 55
chickens and pigs in the pen. There are a total of 178 legs amongst them all. How many pigs are in
the pen?
This problem type shows up as other problems as well. For example, you might find bicycles and tricycles.
| This is a classic guess-and-check problem.
Use this table: (make sure the number of heads adds to 55)
| Guess # | # Chickens | # Pigs | Total
heads | Total
feet |
| 1 | 30 | 25 | 55 | 160 |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
|
|
Prob
& Stat | Problem type: Permutations
Example: 2016 5th grade prob stat #2:
Four students form a line to use a water fountain. How many different ways can they arrange themselves in line?
| This is a permutations problem.
1. The number of ways to pick the first student is ____
2. After picking that student, how many students are left? ____
3. After picking that student, how many students are left? ____
4. How many are left after that pick? ___
5. Multiply these together to get the total number of ways to arrange the students = _____.
|
|
| Number Sense | Problem type: Working backwards
Example: 2016 5th grade number sense #1:
Jason is playing with a stack of cards. He divides the cards into 3 equal piles. Then he takes one pile and divides it into 4 equal piles. Then he takes one of the four equally divided piles and further divides it into 5 equal piles. If one of the five equally divided piles contains 3 cards, how many cards in total are in Jason's stack?
|
This is typical of a whole class of problems that are worked backwards:
1. If Jason has 5 piles at the end and each pile contains 3 cards then those 5 piles contain ____ cards total.
2. If those 5 piles were 1/4 of the cards in the previous step,then the 4 piles together contain ____ cards.
3. Those 4 piles are 1/3 of the deck, so the whole deck contained ____ cards |
|
| Algebra | Problem type: Words into equations
Example: 2017 5th grade algebra #4:
I'm thinking of a number. If I multiply my number by 12 and then add 2, I get the same result as
if I had added 90 to my number. What is my number?
|
This is the standard "Turn words into an equation" problem:
Using N for the number,
1. Write the expression for "multiply my number by 12 and then add 2" = ____________.
2. Write the expression for
"add 90 to my number" = _______.
3. Set these two expressions equal to each other and solve.
N = __________
|
|
| Geometry | Problem type: Cartesian coordinate problems
Example:
2014 5th grade geometry #1:
1) A parallelogram has vertices at
(0, 0), (5, 2), and (1, 3).
The fourth
vertex has positive coordinates. What are they?

|
There are a lot of Cartesian coordinates problems.
This one is typical:
1. Since the opposite sides of a parallelogram are parallel, the third vertex and the 4th vertex are parallel to the first and second.
2. The offset of the second vertex from the first is (___,___).
3. Apply this offset to the third vertex to find the 4th = (___,___).
|
|